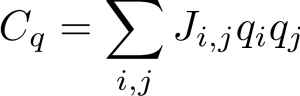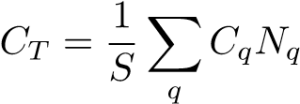AWS Quantum Technologies Blog
How Strangeworks is using Amazon Braket to explore the aircraft cargo loading problem
Quantum computers promise to revolutionize computation for problems across many industrial sectors, though understanding exactly how useful this technology will be remains an open question. In this blog post, the team from Strangeworks, an AWS Partner, evaluates different implementations of the Quantum Approximate Optimization Algorithm (QAOA) against an aircraft cargo loading problem posed by Airbus as part of last year’s Quantum Mobility Challenge. This blog looks at multiple variants of QAOA and a series of benchmarks using the Rigetti Ankaa-3 QPU available via Amazon Braket.
The aircraft cargo loading problem posed by Airbus is a bin packing-style optimization problem that occurs across many industries, including travel, manufacturing, and logistics [1]. These problems are difficult to solve, as the number of possible solutions scales exponentially compared to the number of degrees of freedom in the problem, resulting in a large problem space even for relatively simple optimization problems.
Quantum computing may be well-suited to solve these types of optimization problems, potentially leading to quadratic speedup compared to classical solutions. However, until quantum hardware becomes more mature, heuristic approaches that integrate quantum processing into classical pre-post processing have gained traction. While currently available gate-based quantum hardware does not yet outperform state-of-the-art classical technology, the benchmarking approach shown here delivered accurate results for up to 80 qubit/variable problems.
The QAOA algorithm belongs to the class of hybrid quantum algorithms (leveraging both classical as well as quantum compute), that are widely believed to be a principal method for the current NISQ (noisy intermediate-scale quantum) era. The Strangeworks team built upon two existing QAOA algorithms:
- Standard QAOA, which can be found in many open-source quantum libraries including the Braket algorithm library [2],
- Relax-and-Round QAOA, a variant of QAOA pioneered by the team at Rigetti Computing (QRR QAOA) [3].
As the next section shows, the new StrangeworksQAOA variant, which improves upon the classical processing steps, outperformed the Standard QAOA implementation for this problem and found similar improvements when applying these enhancements to QRR QAOA algorithm.
Using Amazon Braket Hybrid Jobs through the Strangeworks Platform
Combining quantum and classical resources through hybrid algorithms like QAOA offers a pathway to using current quantum computers in tandem with classical workflows. To do so, we make use of Amazon Braket Hybrid Jobs, which allows the entire QAOA workflow to be submitted as a single job. This feature improves the overall runtime, as the algorithm only waits in the Braket internal queue system once, instead of waiting in the queue each time an individual circuit is submitted. Additionally, there are several other features in Braket Hybrid Jobs that save a user time and money. Notably, cached circuit compilation allows any subsequent circuit applied in the workflow to make use of the previous compilation processing if it has a similar structure as the previous circuit.
Users can access Braket, and these features, through the Strangeworks Compute platform. Strangeworks features an online job management system with downloadable software development kits (SDKs), allowing users access to StrangeworksQAOA and Braket Hybrid Jobs, as well as additional quantum, quantum-inspired, and classical devices and solvers.
The scaling of the results as system size grows indicates potential viability for near-term noisy hardware being able to reliably solve larger problems, provided that the right algorithm is used effectively. This combination of the Strangeworks platform, StrangeworksQAOA, Braket Hybrid jobs, and the Rigetti Ankaa-3 device shows a viable path to solving these problems by combining classical resources with quantum hardware.
Benchmarking Approach
To benchmark StrangeworksQAOA, we consider the optimal loading of cargo onto aircraft, originally formulated as part of the Airbus quantum computing challenge [4]. This problem attempts to maximize the mass of the loaded cargo onto an aircraft, while ensuring that the number of containers, n, can fit into the number of available spaces, N. We therefore include constraints, no overlapping containers, and no duplicate containers on board. Following Ref. [5] we formulate this as a Quadratic Unconstrained Binary Optimization (QUBO) problem which we can solve on a quantum computer using the QAOA algorithm [6]. In the benchmarking results, we consider the values for the number of containers, n, and the number of available spaces, N, shown in Table 1.
| Containers, n | Spaces, N | No. of Variables/qubits |
| 5 | 3 | 26 |
| 6 | 4 | 38 |
| 6 | 5 | 46 |
| 7 | 5 | 52 |
| 7 | 6 | 61 |
| 8 | 6 | 68 |
| 8 | 7 | 78 |
Table 1: We consider the following values for the number of containers, n, and the number of available spaces on the aircraft, N. We can then create a QUBO problem with the designated number of variables, which must be encoded on a quantum computer containing that number of qubits.
We apply StrangeworksQAOA through the Strangeworks platform to solve the cargo loading optimization problem discussed in the previous section. In Fig. 1 we compare Standard QAOA [2] (solid squares) and the StrangeworksQAOA algorithm (solid circles), which has had the classical optimization step enhanced and improved. In the Strangeworks approach, we analyze all classical bitstrings that are used to compute the cost function separately and simply store the best-found solution (see next section for technical details).
Additionally, we include results using the Quantum Relax-and-Round (QRR) modification to QAOA from the Rigetti Computing team [3], which improves upon Standard QAOA by optimizing the computation of the cost function (in contrast to StrangeworksQAOA which does not modify the cost function), which results in an improved minimization procedure (dashed squares). During this improved QRR minimization, we can similarly employ the Strangeworks procedure and again keep track of the best single bitstring solution (pink dashed) for no additional computational or monetary cost above standard QRR.
In Fig. 1, StrangeworksQAOA, for both Standard QAOA (solid circles) and QRR (dashed circles) consistently find more favorable solutions across all system sizes considered compared to their respective standard algorithms (squares). Error bars, representing statistical errors in the mean value, for StrangeworksQAOA are smaller than the width of the line showing that results are consistent as well as reliable. We also include the solution found by employing the classical Gurobi solver [7] through the Strangeworks platform. As expected, the Gurobi algorithm finds the optimal solution to the problem, supported by the error bound, or confidence estimate, that Gurobi provides.
![Figure 1: We compare the Rigetti Ankaa-3 quantum computer running the StrangeworksQAOA algorithm (solid circles) to the Standard QAOA algorithm (solid squares), both utilizing the Braket Hybrid Job framework. Additionally, we include results from Rigetti’s QRR version of QAOA (dashed squares) and a StrangeworksQRR (dashed cricles). We use a RealAmplitude circuit for the QAOA ansatz [8]. Note that we average the solution over 8 runs and represent the statistical uncertainty in the mean value with the error bars. For comparison we also include optimal solutions found using the Gurobi algorithm [7] (diamonds). We compare the values of the cost function returned by each algorithm.](https://d2908q01vomqb2.cloudfront.net/5a5b0f9b7d3f8fc84c3cef8fd8efaaa6c70d75ab/2025/08/29/image001-2.png)
Figure 1: We compare the Rigetti Ankaa-3 quantum computer running the StrangeworksQAOA algorithm (solid circles) to the Standard QAOA algorithm (solid squares), both utilizing the Braket Hybrid Job framework. Additionally, we include results from Rigetti’s QRR version of QAOA (dashed squares) and a StrangeworksQRR (dashed cricles). We use a RealAmplitude circuit for the QAOA ansatz [8]. Note that we average the solution over 8 runs and represent the statistical uncertainty in the mean value with the error bars. For comparison we also include optimal solutions found using the Gurobi algorithm [7] (diamonds). We compare the values of the cost function returned by each algorithm.
In Table 2 we use linear regression to fit a straight line to each set of data points for the different algorithms in Fig. 1. This gives us an indication of the scaling of each algorithm line in Fig. 1 as the system size is increased. The differences in the gradients of these lines suggest that if we were to extrapolate to larger system sizes, the lines would begin to deviate more, with bigger discrepancies in the gradients meaning that the results will diverge more quickly. Therefore, because the Strangeworks version of QRR has a gradient that is closest to the exact results (Gurobi), we can infer this will continue to have the smallest errors of the algorithms tested as systems size scales. While these results in Fig 1 indicate for these system sizes considered in this analysis that StrangeworksQAOA shows small errors (~10%), the gradient analysis shows that the errors will continue to get worse if the system size is increased further. This is to be expected and indicates the need for further improvements to all aspects of the workflow, i.e. both the quantum and classical pieces of the algorithm.
| Algorithm | Gradient |
| Gurobi | -1.25 |
| StrangeworksQAOA | 3.47 |
| Standard QAOA | n.a |
| Strangeworks QRR QAOA | -0.16 |
| Rigetti QRR QAOA | 1.06 |
Table 2: We show the gradient of the slope for each algorithm in Fig. 1 upon fitting a line using linear regression to the data. Note that as Standard QAOA scales exponentially (see Fig. 1) it was not possible to obtain a sensible linear fit.
We have found that we can go from noisy results with no meaning (solid squares) to results that closely match the optimal solution (dashed circles). The stark contrast between the worst performing algorithm (solid squares) and the best (dashed cirlces) strongly emphasizes the need for properly optimizing the classical infrastructure surrounding the quantum computation. These algorithms were run on the same device, so all are under the influence of a similar noise model/spectrum. The results indicate that the StrangeworksQAOA algorithm is more robust to inefficiencies surrounding these types of quantum-classical hybrid algorithms, which is a potentially useful property to have if we are to scale up the problem sizes in the future and conduct QAOA experiments on larger hardware devices where noise may play a more prominent role.
StrangeworksQAOA Algorithm Details
The QAOA algorithm is a hybrid classical-quantum algorithm that iterates in a loop between quantum computation and classical processing, see Fig 2. We begin by parameterizing a quantum circuit, U(θ), with a set of classical parameters, θ. In our case, we do not use the Standard QAOA ansatz due to circuit depth limitations of the hardware for the larger problems that we considered. Instead, we use another ansatz commonly used in VQE experiments, the Real Amplitude Quantum Circuit [9] and run the corresponding quantum circuit on Rigetti Ankaa-3 QPU. Note that we use this quantum ansatz for all algorithm versions in this analysis including our “Standard QAOA” implementation. We then measure the resulting qubit states as either in the 0 or 1 states, repeating that experiment many times to obtain a probability distribution. After, we put the probability distribution into a classical function which computes the cost function.
The cost function calculation is the only part of the algorithm that differs between the Standard QAOA and StrangeworksQAOA algorithm as we will see in the next section. Once the cost function has been computed for the quantum circuit with the specified set of variational parameters, the result is put into a classical minimization function, the COBYLA method from the python package SciPy, and the variational parameters are updated. This procedure then iterates many times with the quantum computation facilitating the calculation of the cost function and the classical processing refining the variational parameters until the cost function has been minimized, resulting in the final solution to the problem.
In Standard QAOA, typically, the final answer is found from the measurement results of the final variational circuit, where the most likely bitstring in the probability distribution is chosen as the answer. However, when we consider large system sizes, N, with an exponential number of basis states, 2N, we find that for a realistic and practical number of measurements, the measurements result in a flat probability distribution. This means that each basis state is only measured once, so taking the most likely basis state is not possible. Thus, we take the average cost over all measured basis states as the result for Standard QAOA in Fig 1.
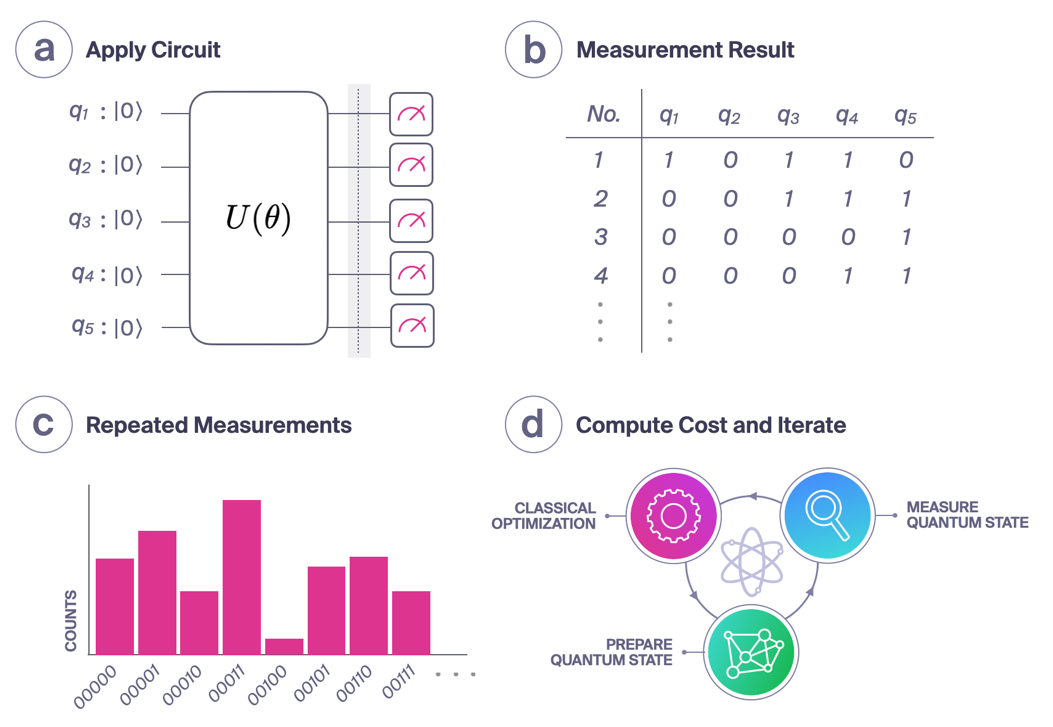
Figure 2: QAOA workflow. (a) First, we set up a circuit with classical variational parameters and apply that circuit to qubits. (b) We then measure the results of that circuit to give us a classical bitstring of 1s and 0s. (c) We repeat that experiment many times (with the same circuit) and create a probability distribution for the measurements. (d) We then calculate the cost, see Eq. 1 & 2, and use a classical optimization algorithm to help us generate a new circuit with a new set of variational parameters. We then iterate between the quantum computer and classical computation to find the optimal quantum circuit that gives rise to the solution with the lowest cost.
In general, QAOA, for the classical calculation of the cost function we take the probability distribution, see Fig 2(c) and the problem QUBO/graph and calculate the cost for each measured basis state separately. For the qth basis state, the cost for that state is,
where the qi ∈{0,1} are the values of the qth bitstring for qubit i and the Ji,j are the coupling values for the problem QUBO/graph. We then calculate the total cost by weighting Cq by the number of times that basis state has been measured, the counts Nq and sum the result giving us an average cost over all the measurement results,
where S is the total number of times the circuit has been measured. In Standard QAOA, the intermediate values for the cost of each basis state, Cq are typically not used and discarded, however see Ref. [10] for some discussion on how to improve this.
In StrangeworksQAOA, we keep track of the smallest Cq and the basis state with the minimum cost throughout all iterations of the algorithm. This smallest cost basis state is then the solution reported by the StrangeworksQAOA algorithm in Fig 1. This basis state selection is a sensible procedure because the solution to the physical cargo loading problem is a classical answer, which is a single basis state. In contrast to common quantum calculations, where we typically calculate averages over the measurement distribution, here we only care about how well we can find the best solution. In Fig 1, we run each version of QAOA algorithm five times to take an average. We see that the statistical error bars are small compared to the width of the lines on the plot for the problem we considered.
Conclusion and Outlook
Our analysis demonstrates the value of optimizing quantum algorithms for specific applications. While standard open-source QAOA implementations provide a useful starting point, carefully tuned approaches like the enhanced StrangeworksQAOA solver can achieve better results in some circumstances without additional computational or financial overhead.
The reliability and reproducibility of our results on the aircraft loading problem suggest a promising path forward. As quantum computing continues to mature, such optimizations will become increasingly important for achieving practical quantum advantage in real-world applications.
To explore these algorithms for your own optimization challenges, visit the Strangeworks platform and documentation on QAOA to get started with Amazon Braket.
References
- Romero, S., Osaba, E., Villar-Rodriguez, E., Oregi, I. & Ban, Y. Hybrid approach for solving real-world bin packing problem instances using quantum annealers. Sci Rep 13, 11777 (2023)
- Farhi, E., Goldstone, J. & Gutmann, S. A Quantum Approximate Optimization Algorithm. arXiv:1411.4028 (2014).
- Dupont, M. & Sundar, B. Extending relax-and-round combinatorial optimization solvers with quantum correlations. PhysRevA.109.012429 (2024)
- Airbus Quantum Computing Challenge https://www.airbus.com/sites/g/files/jlcbta136/files/2021-10/Airbus-QuantumComputing-Challenge-PS5.pdf. Accessed: 2023-07-24.
- Pilon, G., Gugole, N. & Massarenti, N. Aircraft Loading Optimization – QUBO models under multiple constraints. arXiv:2102.09621 (2021).
- Guerreschi, G. G. Solving Quadratic Unconstrained Binary Optimization with divide-and-conquer and quantum algorithms. arXiv:2101.07813v1 (2021).
- Gurobi Optimization https://www.gurobi.com/. Accessed: 2023-07-19.
- QAOA Circuit Ansatz https://qiskit.org/documentation/stubs/qiskit.circuit.library.RealAmplitudes.html Accessed: 2023-07-19.
- Real Amplitude Quantum Circuit Ansatz https://qiskit.org/documentation/ stubs/qiskit.circuit.library.RealAmplitudes.html. Accessed: 2023-08-08.
- Braket QAOA Example https://github.com/amazon-braket/amazon-braket-examples/blob/main/examples/pennylane/2_Graph_optimization_with_QAOA/2_Graph_optimization_with_QAOA.ipynb Accessed: 2023-10-23.