Implementing BB84 Quantum Key Distribution on Amazon Braket: A practical guide

Quantum Key Distribution (QKD) is a method of exchanging encryption keys that complements traditional and post-quantum cryptography by offering a different kind of security guarantee: the ability to reveal whether a key exchange has been observed or disrupted.

This blog explores BB84[i] —the first and most well-known QKD protocol—to illustrate how quantum principles can be used to secure key exchange against undetected interference. The protocol was invented by Charles Bennett and Gilles Brassard in 1984. Its goal is to allow two people (commonly named Alice and Bob) to share a secret key in such a way that no eavesdropper (often called Eve) can learn the key without being revealed.

What makes BB84 unique is that it doesn’t rely on mathematical complexity for its security. Instead, it uses the laws of quantum physics. At its heart, BB84 works by transmitting qubits (commonly mapped into a photon) prepared in randomly chosen quantum states, using one of two complementary bases. Because measuring a qubit in the wrong basis disturbs its state and yields a random result, any eavesdropping attempt introduces detectable errors—allowing Alice and Bob to infer the presence of an eavesdropper during the key exchange.

Here’s the basic idea:

1. Alice randomly chooses qubit states from two different sets of “orientations” (called bases) and sends them to Bob.
2. Bob also randomly selects measurement bases to observe the qubits.
3. After the exchange, Alice and Bob compare which bases they used and only keep the bits where their choices matched.
4. If an eavesdropper tried to intercept the qubits, their presence would introduce detectable errors due to the nature of quantum measurements.

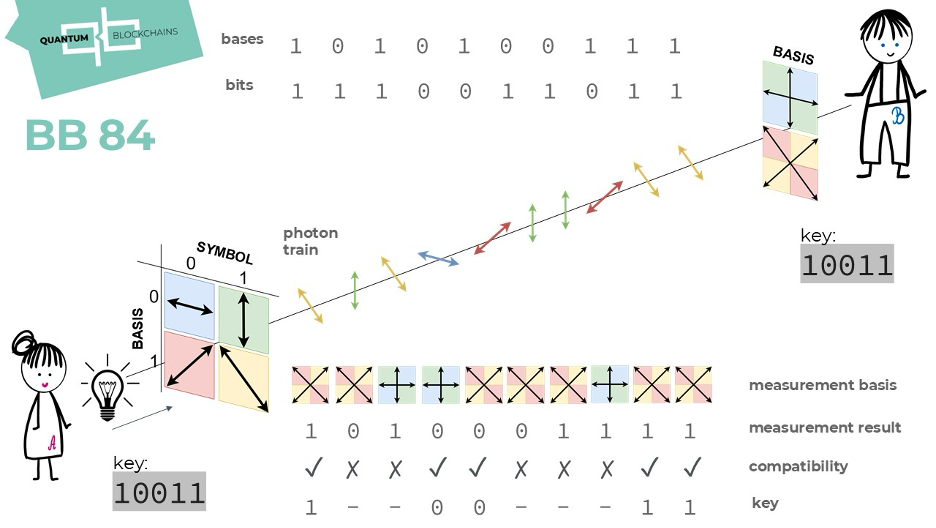
Figure 1 – Schematic representation of quantum key distribution using the BB84 protocol. Picture by Dr. Marta Misiaszek-Schreyner.

This simple yet powerful mechanism enables the creation of a shared secret key that is provably secure—something not possible with classical communication alone. This technical guide demonstrates a complete implementation of BB84 on Amazon Braket, exploring the protocol’s crucial components: quantum state preparation in conjugate bases, measurement basis selection, sifting, error estimation, and key reconciliation. You’ll see how Braket’s quantum circuit primitives are used to encode quantum states, apply basis transformations, and carry out the classical post-processing needed for secure key generation.

For those interested in reproducing or modifying the implementation, the full source code is available in the AWS Samples GitHub repository[ii]. The functions used throughout the blog, including initialize_protocol() and measure_qubits(), are defined in the utils/bb84.py[iii] file and can be easily adapted for experimentation.

Beyond the basic protocol logic, we also examine practical factors such as quantum channel noise and measurement errors, discussing how they influence the final key rate. This implementation serves both as a hands-on introduction to quantum cryptography and as a benchmark for evaluating the strengths and constraints of quantum computing platforms in real-world cryptographic contexts.

Why use error correction in BB84?

Even under ideal conditions, quantum communication is susceptible to noise and imperfections in measurement. In practical settings, environmental factors and quantum channel characteristics introduce errors that can cause discrepancies between the keys generated by Alice and Bob. To ensure both parties arrive at an identical and secure shared key, the BB84 protocol incorporates an error correction phase using classical methods. In our implementation, we use the [24,12,8] Golay code to detect and correct these errors efficiently. We introduce the details of this code later in the blog.

Implementation dependencies and configuration

Our BB84 implementation relies on a few library dependencies that balance practical implementation needs with a quantum simulation. The Braket SDK provides essential quantum circuit manipulation and simulation tools, while custom utility modules (bb84, golay_code, and secret_utils) encapsulate protocol-specific operations to maintain clean separation of concerns.

The configuration parameters are chosen to demonstrate a realistic QKD scenario while remaining computationally tractable:

• BIT_FLIP_PROBABILITY models quantum channel noise and potential eavesdropping attempts. The value of 0.1 represents a practical compromise between realistic noise levels and the protocol’s error correction capabilities. The implementation remains stable up to approximately 0.25, beyond which key reconciliation becomes increasingly challenging.
• NUMBER_OF_QUBITS is set to 12 to align with the [24,12,8] Golay code (see upcoming discussion), which operates on 12-bit blocks. While smaller values would work just the same, we use 12 because it’s the maximum supported by the Braket local simulator with noise (braket_dm). This lets us maximize the key size for our demonstration.
• ERROR_CORRECTION_CHUNK_SIZE = 12 matches our Golay code block size, ensuring efficient error correction processing. Modifying this value would require corresponding changes to the error correction implementation and could impact the protocol’s ability to generate secure keys.

Lastly, we initialize empty arrays alice_raw_key and bob_raw_key as NumPy arrays to facilitate efficient bit manipulation and statistical analysis during the key reconciliation phase. This choice of data structure supports both the quantum and classical post-processing stages of the protocol.

The bb84 module that follows handles the quantum operations, including the random generation of bit values and measurement bases, the encoding of qubits into quantum circuits, and their measurement and sifting. This is where we simulate the core quantum exchange between Alice and Bob, managing how qubits are prepared, transmitted, and filtered based on basis alignment.

import base64
import numpy as np

from braket.circuits import noises
from braket.devices import LocalSimulator

from utils.bb84 import initialize_protocol, encode_qubits, measure_qubits, filter_qubits, array_to_string
from utils.golay_code import GolayCode
from utils.secret_utils import convert_to_octets 

BIT_FLIP_PROBABILITY = 0.1 
NUMBER_OF_QUBITS = 12
ERROR_CORRECTION_CHUNK_SIZE = 12

alice_raw_key = np.array([])
bob_raw_key = np.array([])

The Golay code in BB84

The mathematical elegance of the [24,12,8] Golay code makes it a natural choice for QKD applications. As a perfect ternary code achieving the Hamming bound[iv], it maximizes the use of coding space while providing robust error correction capabilities. The code transforms 12-bit messages into 24-bit codewords, maintaining a Hamming distance of 8 between valid codewords. This structure allows it to correct up to 3 errors in each block while detecting up to 7 errors – a crucial feature when dealing with quantum channel noise and potential eavesdropping attempts.

The code’s 1:2 rate might seem like a significant overhead, but it’s a necessary trade-off in quantum implementations. Quantum channels typically exhibit both random and burst errors, and the [24,12,8] Golay code is widely recognized for its strong correction performance in such conditions. With our chosen bit-flip probability of 0.1, the code operates well within its correction capacity, ensuring reliable key reconciliation[v] while maintaining a practical final key rate.

From theory to implementation: BB84 protocol flow

While BB84 was originally conceived for optical quantum cryptography implementations, our choice to use quantum computing circuits offers compelling advantages for both research and development purposes. The approach builds on the fundamental equivalence between quantum information processing platforms while providing powerful tools for protocol analysis and development.

Quantum circuits provide a mathematical framework for demonstrating BB84’s core principles. Key operations in the protocol have direct analogues across optical and circuit-based implementations: preparing |0⟩ and |1⟩ states corresponds to photon polarization, and Hadamard gates mimic polarization rotations for basis changes. While physical setups and practical challenges differ, both models rely on the same underlying quantum mechanics that ensures BB84’s security.

In our implementation, the Braket density matrix local simulator (braket_dm) to model the protocol. Rather than simulating a full optical channel with photon loss and timing effects, we apply noise directly to the quantum states via gate operations. Specifically, we introduce bit-flip noise, which closely mirrors polarization drift in optical systems — effectively flipping the measured state, like an X gate. We avoid more general noise models like depolarizing noise, since BB84 discards mismatched basis measurements, making phase errors largely irrelevant. This approach keeps the simulation focused and physically meaningful while still capturing the protocol’s behavior under imperfect conditions.

Key generation loop: building raw key material

Our BB84 implementation iteratively builds a secure raw key through repeated quantum state exchanges until reaching the required 12-bit threshold. Each iteration runs a complete cycle of the protocol, structured in four phases.

The following functions define the core quantum operations that simulate Alice’s and Bob’s roles in the protocol:

def initialize_protocol(number_of_qubits):
    encoding_basis = np.random.randint(2, size=number_of_qubits)
    alice_states = np.random.randint(2, size=number_of_qubits)
    measurement_basis = np.random.randint(2, size=number_of_qubits)
    return encoding_basis, alice_states, measurement_basis

This function randomly generates the bitstring Alice wants to encode (alice_states), her choice of encoding basis (encoding_basis), and Bob’s measurement basis (measurement_basis). The randomness of these values is fundamental to BB84’s security assurance .

def encode_qubits(number_of_qubits, alice_states, encoding_basis):
    circuit = Circuit()
    for idx in range(len(encoding_basis)):
        if alice_states[idx] == 1:
            circuit.x(idx)
        else:
            circuit.i(idx)
        if encoding_basis[idx] == 1:
            circuit.h(idx)
    return circuit

Each qubit is initialized with a combination of Pauli-X and Hadamard gates depending on the bit value and the basis. This creates the quantum state that Alice would send across the channel.

def measure_qubits(circuit, measurement_basis):
    for i in range(len(measurement_basis)):
        if measurement_basis[i] == 1:
            circuit.h(i)
    return circuit

On Bob’s side, Hadamard gates are applied to any qubit where he chose a diagonal basis. This aligns the measurement operation with his randomly chosen basis.

With these quantum primitives defined, we can now simulate the full BB84 protocol using Braket’s local density matrix simulator.

while len(alice_raw_key) < ERROR_CORRECTION_CHUNK_SIZE:
    # Phase 1: Initialize quantum states and bases
    encoding_basis_A, states_A, _ = initialize_protocol(NUMBER_OF_QUBITS)
    _, _, measurement_basis_B = initialize_protocol(NUMBER_OF_QUBITS)

In each round, Alice and Bob independently generate random bases. Alice prepares a random bitstring and selects a basis (rectilinear or diagonal) for each qubit. Bob likewise chooses a basis for measurement. This independence is fundamental to BB84: without prior coordination, any eavesdropping attempt becomes statistically detectable.

    # Phase 2: Quantum state preparation and transmission
    encoded_qubits_A = encode_qubits(NUMBER_OF_QUBITS, states_A, encoding_basis_A)
    noise = noises.BitFlip(probability=BIT_FLIP_PROBABILITY)
    encoded_qubits_A.apply_gate_noise(noise)

Alice encodes her qubits using a combination of X and H gates based on the generated values. We simulate channel noise using a bit-flip error model, where each qubit is randomly flipped with 10% probability. This simplified model captures the dominant type of noise in polarization-based BB84 implementations — namely, basis misalignment or polarization drift, which correspond to logical X errors.

While this does not model the full range of optical channel effects (such as photon loss, dispersion, or phase errors), it provides a meaningful and efficient proxy to test BB84’s robustness under realistic conditions. The selected noise level (10%) is also just below BB84’s maximum tolerable error rate[vi] (~11%), ensuring that our error correction stage has practical relevance.

    
    # Phase 3: Measurement
    measured_circuit = measure_qubits(encoded_qubits_A, measurement_basis_B)
    device = LocalSimulator("braket_dm")
    result = device.run(measured_circuit, shots=1).result()
    measured_bits = list(result.measurements[0])

Bob measures each qubit in his chosen basis. If his basis differs from Alice’s, the outcome will be random; if it matches, he should observe Alice’s bit — unless noise has introduced an error. The use of Braket’s density matrix simulator (braket_dm) allows us to accurately model noisy quantum behavior across the circuit, including gate noise and measurement statistics.

    # Phase 4: Basis reconciliation and key sifting
    alice_raw_key = np.concatenate((alice_raw_key, filter_qubits(sent_bits, encoding_basis_A, measurement_basis_B)))
    bob_raw_key = np.concatenate((bob_raw_key, filter_qubits(measured_bits, encoding_basis_A, measurement_basis_B)))

Finally, we perform basis reconciliation and key sifting. The filter_qubits() function compares Alice’s and Bob’s bases and keeps only the bits where they match — typically about half of the qubits. These retained bits form the sifted key, which grows with each iteration of the loop. Once we reach 12 matching bits, we move on to error correction.

This explains why we set NUMBER_OF_QUBITS = 12: since only ~50% of the qubits survive basis sifting, multiple rounds are needed to accumulate enough usable key material. The loop structure efficiently handles this while preserving BB84’s core security properties.

Raw key generation results

Examining our raw key outputs reveals a very high correlation between Alice and Bob’s bits, as expected. Both parties have generated highly correlated, however not identical, 12-bit sequences:

alice_raw_key = alice_raw_key[:12] 
alice_raw_key
array([0., 0., 1., 1., 0., 1., 0., 1., 1., 0., 0., 1.])
bob_raw_key = bob_raw_key[:12] 
bob_raw_key
array([0., 0., 1., 1., 0., 0., 0., 1., 1., 1., 0., 1.])

In a flawless quantum setup without any noise or losses, we would observe a perfect correlation between Alice’s and Bob’s raw keys. However, in real-world QKD this is rarely the case. This is why in our implementation we introduced the 10% bit-flip probability – to introduce some discrepancies between raw keys on both exchange sides and in this way model the real-life faults. This is also precisely why BB84 incorporates error correction in its next phase.

Key reconciliation

After basis sifting yields matching raw key segments, we enter the critical phase of key reconciliation. This stage addresses the quantum channel noise and potential eavesdropping effects that may have created discrepancies between Alice and Bob’s raw keys. Our implementation uses a [24,12] linear code for error correction, providing a robust mechanism to detect and correct discrepancies between the keys while minimizing information leakage.

The reconciliation process begins by instantiating the error correction framework:

error_correcting_code = GolayCode()
generator_matrix = error_correcting_code.get_generator_matrix()
parity_check = error_correcting_code.get_parity_check_matrix()
b_matrix = error_correcting_code.get_b_matrix()

These matrices define the algebraic structure of our error correction scheme. The generator matrix maps our 12-bit raw key segments into 24-bit codewords, providing redundancy for error detection and correction. The parity check matrix is used to compute the syndrome – a mathematical indicator that reveals the presence and location of errors in the key. When applied to a valid key, the syndrome calculation results in all zeros, while any ones in the output indicate errors that need correction. The B-matrix facilitates efficient decoding operations. Together, these components implement a perfect ternary code capable of correcting up to three errors in each 24-bit block—a capability that proves crucial given our channel’s 10% error probability.

On Alice’s side, the process begins with encoding her 12-bit raw key into a 24-bit codeword using the generator matrix. When Alice performs the syndrome calculation through modulo-2 matrix multiplication, she should get all zeros, indicating a valid codeword without errors:

encoded_key_A = np.matmul(generator_matrix, alice_raw_key) % 2
syndrome_A = np.matmul(encoded_key_A, parity_check) % 2
parity_bits = encoded_key_A[12:]

The presence of zeros in Alice’s syndrome confirms the integrity of her encoding process. Only the parity bits (positions 12-23) are transmitted to Bob, preserving the security of the actual key bits.

print(f'Key of Alice after encoding is: {encoded_key_A}')
print(f'Syndrome of Alice (should be all zero): {syndrome_A}')
print(f'Information sent to Bob: {parity_bits}')
 

(Output):

Key of Alice after encoding is: [0. 0. 1. 1. 0. 1. 0. 1. 1. 0. 0. 1. 1. 0. 0. 1. 0. 0. 0. 1. 0. 1. 1. 1.]

Syndrome of Alice (should be all zero): [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]

Information sent to Bob: [1. 0. 0. 1. 0. 0. 0. 1. 0. 1. 1. 1.]

On Bob’s side, the syndrome serves a more complex purpose. After receiving Alice’s parity bits, Bob performs two syndrome calculations:

encoded_key_B = np.concatenate((bob_raw_key, parity_bits))
syndrome_B = np.matmul(encoded_key_B, parity_check) % 2
syndrome_BB = np.matmul(syndrome_B, b_matrix) % 2

print(f"Encoded key at Bob's: {encoded_key_B}")
print(f"First syndrome: {syndrome_B}")
print(f"Second syndrome: {syndrome_BB}")
 

(Output):

Encoded key at Bob’s: [0. 0. 1. 1. 0. 0. 0. 1. 1. 1. 0. 1. 1. 0. 0. 1. 0. 0. 0. 1. 0. 1. 1. 1.]

First syndrome: [0. 0. 1. 1. 1. 1. 0. 0. 0. 1. 1. 0.]

Second syndrome: [0., 0., 0., 0., 0., 1., 0., 0., 0., 1., 0., 0.]

The interpretation of these syndromes is crucial: If Bob’s syndromes are all zeros (matching Alice’s), it indicates that his key perfectly aligns with Alice’s. If any ones appear in the syndrome, they indicate the presence and location of errors in Bob’s key. We assume that the classical connection is error-free, therefore errors can only occur as the result of imperfect quantum exchange, i.e. on the first 12 bits, and no errors are present in the parity bits. In this case, the second syndrome calculation (syndrome_BB) transforms the error information into a format that directly maps to the positions needing correction. When errors are detected (indicated by ones in the syndrome), the correction process generates a mask based on the syndrome values:

if syndrome_BB.sum() < 4:
    correction_mask = np.concatenate((syndrome_BB, np.zeros(12,)))
    print(correction_mask)
else:
    print("Decoding failed - more than 3 errors")

(Output):

[0. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]

The final reconciliation step applies this correction mask to Bob’s raw key through modulo-2 addition, enabling error correction without transmitting the actual key bits:

corrected_key = np.mod(bob_raw_key + correction_mask[:12], 2)
corrected_key

(Output):

array([0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1])

The verification shows that Bob’s corrected key now matches Alice’s raw key:

corrected_key == alice_raw_key

(Output):

array([ True,  True,  True,  True,  True,  True,  True,  True,  True,  True,  True,  True])

From a security perspective, this implementation achieves an elegant balance. By transmitting only parity bits and using syndrome-based error correction, we can detect and correct up to three errors per block while minimizing information exposed to potential eavesdroppers. While our example shows direct comparison of the final keys, in practice, a hash function would be used for verification to avoid exposing the entire key content. The successful reconciliation demonstrated here confirms the effectiveness of our approach in ensuring reliable key distribution even across noisy quantum channels.

Conclusion

The process of generating raw key material through quantum state encoding, transmission, and reconciliation lies at the core of QKD protocols. Each phase represents a step towards achieving a secure, shared key that can withstand potential security threats, such as eavesdropping. This fundamental approach to key distribution exemplifies the power and promise of quantum cryptography in enabling secure communications.

However, implementing BB84 in real-world scenarios presents several significant challenges. Quantum state preparation and detection are highly sensitive to environmental factors, with temperature fluctuations and mechanical vibrations potentially increasing error rates beyond the correction capabilities of our reconciliation scheme. The maximum distance between Alice and Bob is limited by photon loss in optical fibers, typically restricting practical QKD systems to distances of 100-150 kilometers without quantum repeaters. Additionally, timing synchronization between the parties must be extremely precise, often requiring atomic clocks for accurate photon detection windows.

Our implementation, performed on Braket’s density matrix simulator, demonstrates the BB84 protocol using a simplified bit-flip noise model and shows the effectiveness of linear error-correcting codes in key reconciliation, successfully handling up to three-bit errors. While this abstraction helps illustrate the key reconciliation process, real QKD systems face different types of noise and practical challenges. Unlike our simulation where noise is introduced through controlled bit flips, physical QKD implementations must contend with photon loss in optical fibers (the primary limiting factor), dark counts in single-photon detectors, timing jitter, phase instability in interferometers, and polarization drift. Despite these simplifications, our implementation successfully demonstrates the core principles of quantum key distribution and error correction, though practical QKD systems must carefully balance their error correction capability against security requirements based on actual channel characteristics and noise levels. The next crucial step after successful reconciliation would be privacy amplification to reduce any partial information an eavesdropper might have gained during the reconciliation process.

As quantum computing hardware continues to evolve and quantum memory technologies improve, these implementation challenges are gradually being addressed. The development of quantum repeaters and more efficient error correction protocols promises to extend the reach and reliability of QKD systems, bringing us closer to widespread deployment of quantum-secure communication networks.

Quantum Blockchains take the challenges of QKD protocol implementation and integration into real-world digital networks very seriously. To address these complexities, the company developed a QKD emulator that uses post-quantum key exchange mechanisms for simulation of key distribution[vii]. This emulator served as the foundation for the Quantum Cryptography Migration System (QCMS)[viii], a service designed to streamline the transition from emulated to genuine QKD—significantly accelerating deployment timelines. As a next step, the company created a Digital Twin of the QKD emulator and made it available via the AWS Marketplace[ix]. This solution enables post-quantum secure VPN connectivity to Amazon VPC, providing a practical and scalable approach to quantum-ready networking in the cloud.

During the research leading to this post, Quantum Blockchains released an initial version of the code in Qiskit[x]. Additionally, the company devised a network topology for blockchains based on hypercube principles, enabling the creation of realistic blockchain infrastructures with QKD-secured data-in-motion[xi]. In another thread, the research team at Quantum Blockchains conceptualized a quantum network leveraging a Conference Key Agreement (CKA) protocol, which paves the way for a far more reliable consensus mechanism for blockchains[xii]. You can check the website for more details.

References

[i] Bennett, C. H., & Brassard, G. (2020). Quantum cryptography: Public key distribution and coin tossing. arXiv:2003.06557 [quant‑ph]. (Reprint of the original 1984 BB84 protocol paper with modern typesetting). https://arxiv.org/abs/2003.06557

[ii] AWS Samples. (2025). BB84 QKD Protocol on Amazon Braket [GitHub repository]. https://github.com/aws-samples/sample-BB84-qkd-on-amazon-braket

[iii] AWS Samples. (2025). BB84 QKD Protocol on Amazon Braket – bb84.py [Source code]. https://github.com/aws-samples/sample-BB84-qkd-on-amazon-braket/blob/main/utils/bb84.py

[iv] Wikipedia contributors. (2023). Hamming bound. Wikipedia. https://en.wikipedia.org/wiki/Hamming_bound

[v] Elkouss, D., Leverrier, A., Alléaume, R., & Boutros, J. (2009). Efficient reconciliation protocol for discrete‑variable quantum key distribution. arXiv:0901.2140 [cs.IT] https://arxiv.org/abs/0901.2140

[vi] Shor, P. W., & Preskill, J. (2000). Simple Proof of Security of the BB84 Quantum Key Distribution Protocol. arXiv:quant‑ph/0003004. https://arxiv.org/abs/quant-ph/0003004 (Also published as Phys. Rev. Lett. 85, 441–444, 2000).

[vii] Quantum Blockchains – Post-Quantum Key Distribution (pQKD) landing page. A groundbreaking cybersecurity solution designed to accelerate the transition towards quantum-resistant cryptographic systems. [Website] https://www.quantumblockchains.io/pqkd/

[viii] Quantum Blockchains – Quantum Cryptography Migration System (QCMS) – Seamless and Cost-Efficient Transition to Quantum Cryptography [Website] https://www.quantumblockchains.io/qcms/

[ix] AWS Marketplace: pQKD Twin Cloud Edition with VPN (deployed in AWS) – A Quantum-Resistant VPN for AWS – Secure your AWS cloud VPC with cutting-edge post-quantum encryption, genuine quantum entropy (QRNG), and ETSI QKD compatibility. [Website] https://aws.amazon.com/marketplace/pp/prodview-bmd5siosuuaze

[x] Kosik, M. (2023). QKD Protocol Simulation with Qiskit. Quantum Blockchains.  https://www.quantumblockchains.io/qkd-protocol-simulation-with-qiskit/

[xi] Marta Misiaszek-Schreyner, Łukasz Kujawski, Miriam Kosik, Piotr Kulicki, Mirek Sopek, and others (2023). Quantum Blockchain Consensus with Key Distribution (QBCK) [White Paper]. Quantum Blockchains. https://quantumblockchains.io/wp/QBCK_WhitePaper.pdf

[xii] Misiaszek‑Schreyner, M., Kosik, M., & Sopek, M. (2023). Time‑Bin CKA as a tool for blockchain technology. arXiv:2308.16289 [cs.CR]. https://arxiv.org/abs/2308.16289