Quantum-Guided Cluster Algorithms for Combinatorial Optimization

This post was contributed by Peter Eder, Aron Kerschbaumer, Jernej Rudi Finžgar, Raimel Medina, Martin Schuetz, Helmut Katzgraber, Sarah Braun, and Christian Mendl.

Optimizing complex systems is a major challenge in science and industry. Many tasks – such as scheduling, routing, portfolio selection, or network design – can be written as combinatorial optimization problems that are simple to describe but very hard to solve, often trapping local search in difficult landscapes.

Motivated by the practical importance and computational hardness of such problems, recent years have seen a surge of interest in using alternative computational paradigms. Among the most promising is quantum computing, whose algorithms can encode nontrivial information that is difficult to reproduce classically. Exploring how to best utilize those in order to form good solutions, led to a spectrum of quantum-informed optimization strategies that aim to guide classical heuristics with richer problem insight. You can see an example of this in a previous post about Quantum-Informed Recursive Optimization Algorithms (see also [1]).

In this work, we introduce the quantum-guided cluster algorithm (QGCA), which uses precomputed correlations – such as those obtained from quantum optimization algorithms – to guide collective spin updates and reach good solutions more quickly. The idea is to use quantum information to identify and flip groups of spins (clusters) with a high chance of acceptance. We demonstrate the approach with correlations from the Quantum Approximate Optimization Algorithm (QAOA) [2], showing on certain graph instances that quantum-guided clusters explore the solution space more effectively and outperform simulated annealing, a well-known classical heuristic. This hybrid workflow illustrates a practical way to utilize quantum-derived structure for difficult optimization problems with constraints and frustration.

Quantum optimization for constrained problems

A common first step in both classical and quantum optimization is to express the problem as a quadratic unconstrained binary optimization (QUBO) problem. In a QUBO, we encode a candidate solution by binary variables x_i and define a quadratic cost function:

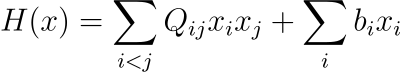
where the coefficients Q_ij and b_i describe the problem. Although the formulation is called “unconstrained”, constraints are typically enforced by adding penalty terms that penalize solutions, not fulfilling the constraints. Choosing these penalties is tricky: too small, and infeasible solutions slip through; too large, and the search space becomes distorted and harder to explore.

A particularly useful benchmark problem is Max-Cut. Given a weighted graph, the goal is to partition the vertices into two sets such that the total weight of edges crossing between the sets is maximized. Max-Cut is not just a toy example: it can represent tasks like circuit layout design, portfolio balancing, and scheduling. Moreover, many other combinatorial problems – such as maximum independent set, graph coloring, and certain clustering formulations – can be mapped into Max-Cut. This makes it a standard target for testing both classical heuristics and quantum methods (see [3, 4]).

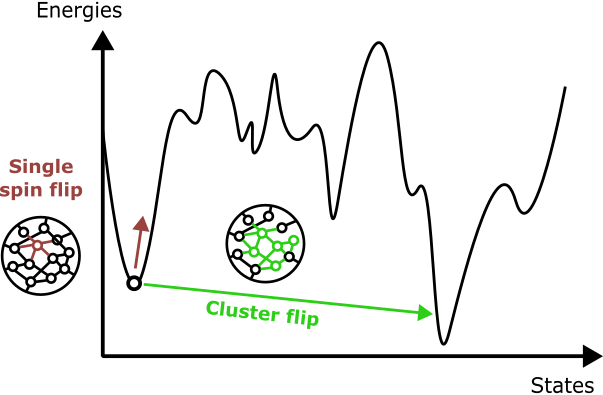
Figure 1 : A rugged energy landscape, characteristic of combinatorial optimization problems, is depicted, along with illustrative transitions from single-spin-flip and cluster-flip updates.

On the classical side, simulated annealing is a well-known baseline. It makes small, local moves (for example, flipping a single variable), and controls the acceptance of worse solutions using a “temperature” parameter that is gradually reduced. This works well for many smooth optimization landscapes, but it struggles on problems with rugged structure – landscapes with many local minima separated by large barriers. In these cases, single-spin updates can easily get stuck far from the global optimum. This is illustrated in Figure 1.

To address this, researchers developed cluster algorithms that flip many variables at once. Two prominent examples are the Swendsen-Wang [5] and Wolff [6] algorithms, which group together correlated variables and flip entire clusters. These methods are very effective for special cases such as ferromagnetic systems, where variables naturally align into large uniform regions, making collective moves extremely powerful. Another influential approach is the Houdayer algorithm [7], which introduces cluster updates between pairs of replicas of the system and has been shown to accelerate equilibration in certain low-dimensional settings.

However, when applied to more general optimization problems, especially those with conflicting constraints (where not all spins can be satisfied simultaneously), these cluster methods lose their advantage. Instead of forming meaningful local groups, clusters either grow too large – covering nearly the whole system – or fail to capture useful structure. As a result, they do not reliably improve over simpler single-variable updates on complex, frustrated optimization tasks.

Quantum-Guided Cluster Algorithms

To address the limitations of simulated annealing and traditional cluster updates on hard optimization problems, in this work we propose a quantum-guided cluster algorithm (QGCA) (see Figure 2). The central idea is to retain the efficiency of collective spin flips, while avoiding the percolation issues that make existing cluster algorithms ineffective on frustrated optimization problems (for example, optimization problems with conflicting constraints).

The algorithm works as follows: before the optimization run begins, we compute pairwise correlations between variables. These correlations can come from different sources – directly from the problem couplings, from classical approximation methods such as semidefinite programming or Monte Carlo sampling, or from quantum algorithms like QAOA that prepare low-energy states. The resulting correlation matrix contains information about how spins tend to align in good solutions.

Figure 2 : A high-level scheme of the cluster algorithm, showing the individual steps performed in every iteration until the final temperature is reached. Note that the correlations must be calculated only once at the beginning. First, a random spin configuration is initialized. Then in each iteration, a cluster is built, using the information from the precomputed correlations in the form of a matrix Z. This cluster is flipped and accepted or rejected according to the same rule as the one used in simulated annealing (Metropolis criterion). Then the temperature is lowered in order to ensure convergence to an optimum.

During optimization, we build clusters by starting from a random variable and probabilistically adding neighbors according to their correlation strength. This ensures that clusters reflect meaningful structure rather than random connectivity. Once a cluster is formed, all variables in it are flipped together, and the move is accepted or rejected using the same temperature-based rule as in simulated annealing. In this way, the algorithm can make large, targeted jumps through the search space, rather than being restricted to small, local moves.

Importantly, this mechanism avoids the pitfalls of earlier cluster approaches. Because cluster formation is guided by correlation data rather than geometry alone, clusters do not blow up to system-spanning size and remain useful even in highly constrained or frustrated settings. At the same time, the use of correlation information injects a global structure into what is otherwise a purely local search process.

More details on the specific correlation sources and the cluster-building rules can be found in the paper [8].

Experiments

We evaluated the algorithm using quantum-derived correlations to assess their effectiveness in guiding cluster updates. Specifically, we used correlations from QAOA circuits simulated classically using a CUDA-accelerated simulation framework for QAOA called CUAOA [9]. For reference, we also compared them to our cluster algorithm guided by coupling constants only (no additional information despite the graph itself).

Figure 3 shows results on ten-regular Max-Cut graphs with 28 nodes. At depth p=1, QAOA, which can still be simulated efficiently on a classical computer, performs very similar to the coupling-constant baseline. Once the depth is increased to p=2, however, the QAOA correlations begin to improve the cluster building process and yield better solution quality than couplings alone. Note that simulated annealing (not shown here) is also outperformed by the QGCA, using correlations from p=2 QAOA. This trend continues up to p=10.

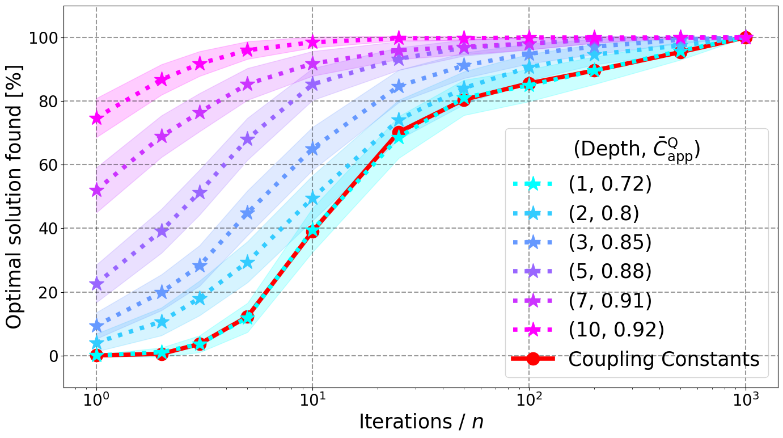
Figure 3 : The performance of the cluster algorithm for 10-regular graphs of size n=28, guided by QAOA correlations at various depths (1, 2, 3, 5, 7, 10), which lead to different average approximation ratios〖 C ̅〗_app^Q ( qualities of solutions that are used to calculate the correlations). One can see that for depth one, the performance of the QGCA (cyan line) closely resembles that of the coupling constants (red line) and that the performance improves with higher layers.

Although these are still small problem sizes, the experiments are encouraging: they demonstrate that quantum optimization algorithms can provide information that translates into measurable performance gains in our cluster algorithm.

Finally, to demonstrate that the cluster algorithm outperforms a well-established classical heuristic – simulated annealing – we evaluated its performance on larger graphs with . The results are presented in Figure 4. For three-regular graphs, the algorithm, when guided by coupling constants or random correlations, clearly surpasses simulated annealing. In contrast, for 20-regular graphs, simulated annealing slightly outperforms the coupling-constant approach. This behavior can be attributed to the higher degree of frustration in dense graphs, which causes the coupling constants to provide misleading guidance. Nevertheless, as shown in the paper, graphs with higher frustration exhibit the greatest performance gains, thus outperforming simulated annealing, when supplied with low-energy correlations.

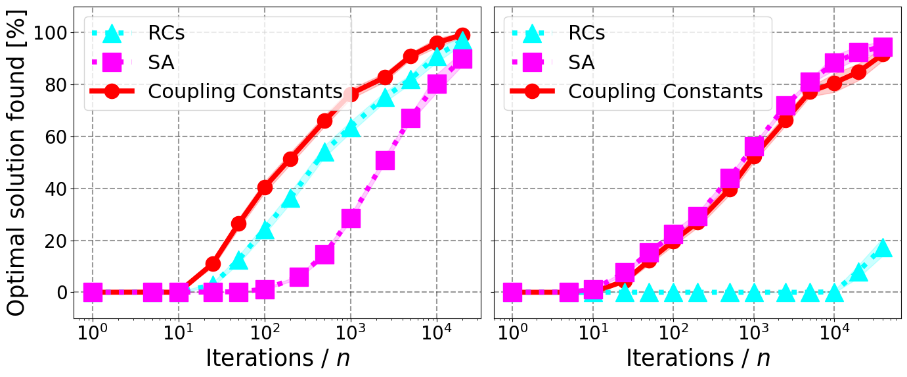
Figure 4 : The performance of the cluster algorithm is evaluated for regular-degree graphs of size n=100 with degree three (left) and degree 20 (right), guided by coupling constants ( no additional information despite the graph itself) and random correlations (RCs). The plot further shows the performance of simulated annealing (SA).

Outlook – call to action

The results demonstrate that correlation-guided cluster algorithms are a promising route for tackling hard combinatorial optimization problems. By utilizing low-energy correlations, they enable collective moves that remain effective even in highly constrained and frustrated settings, where standard methods struggle. At the same time, it remains to be seen how the approach scales to larger and more complex problem instances, which will be critical for practical impact. Ultimately, realizing the full potential of QGCA will depend on the continued progress of quantum hardware, as larger and more reliable devices are needed to supply high-quality correlations at scale.

There are multiple promising extensions for future work, such as modifying the cluster-building procedure to align more closely with Markov chain Monte Carlo methods, ensuring properties such as ergodicity and detailed balance, which would broaden its applicability. Furthermore, benchmarking the algorithm against correlations obtained from alternative quantum methods, such as Variational Quantum Eigensolvers or Quantum Annealing, could provide deeper insights into the comparative advantages of different approaches. Another important question is whether filtering correlations – such as considering only the lowest-energy bitstrings – could improve the quality of the guiding information. Moreover, the effects of noise in the Noisy Intermediate-Scale Quantum (NISQ) era should be analyzed.

Potential applications are broad, ranging from scheduling and logistics to portfolio optimization and network design – domains where rugged search landscapes and hard constraints are the norm. We view our work as an encouraging first step, and we look forward to future studies that will explore the full potential of correlation-guided approaches in these real-world settings.

References

[1] Finžgar, J. R., Kerschbaumer, A., Schuetz, M. J. A., Mendl, C. B., and Katzgraber, H. G., “Quantum-Informed Recursive Optimization Algorithms”, arXiv:2308.13607.

[2] Farhi, E., Goldstone, J., and Gutmann, S., “A Quantum Approximate Optimization Algorithm”, arXiv:1411.4028.

[3] Lucas, Andrew. 2014. ‘Ising Formulations of Many NP Problems’. Frontiers in Physics 2. doi: 10.3389/fphy.2014.00005.

[4] Glover, F., Kochenberger, G., and Du, Y., “A Tutorial on Formulating and Using QUBO Models, arXiv:1811.11538.

[5] R. H. Swendsen and J.-S. Wang, “Nonuniversal critical dynamics in monte carlo simulations,” Physical Review Letters, vol. 58, no. 2, p.86–88, 1987.

[6] U. Wolff, “Collective monte carlo updating for spin systems,” Physical Review Letters, vol. 62, no. 4, p. 361–364, 1989.

[7] J. Houdayer, “A cluster monte carlo algorithm for 2-dimensional spin glasses,” The European Physical Journal B, vol. 22, no. 4, p. 479–484, 2001.

[8] Eder, P. J., Kerschbaumer, A., Finžgar, J. R., Medina, R. A., Schuetz, M. J. A., Katzgraber, H. G., Braun, S., and Mendl, C. B., “Quantum-Guided Cluster Algorithms for Combinatorial Optimization”, arXiv:2508.10656, 2025.

[9] Stein, J., Blenninger, J., Bucher, D., Eder, P. J., Çetiner, E., Zorn, M., and Linnhoff-Popien, C., “CUAOA: A novel CUDA-accelerated simulation framework for the QAOA”, arXiv:2407.13012.