AWS Quantum Technologies Blog
AWS Collaborates with Chugai Pharmaceutical Co. on Quantum-Inspired and Constraint Programming Methods for Cyclic Peptide-Protein Docking
Given a three-dimensional model of a drug’s potential target (the binding site), what is the orientation of the drug candidate molecule that best “fits” (docks onto) this binding site? Structure-based drug design involves the use of computational tools to answer this very question!
Chugai Pharmaceutical Co., Ltd., a leading Japanese pharmaceutical company, specializes in the research, development, manufacturing, and marketing of prescription medications targeting oncology, immunology/allergy, neurology, and renal diseases. In its pursuit to advance molecular research through quantum computing technology, Chugai engaged with Amazon Web Services (AWS) to explore the application of quantum-amenable computing techniques to docking simulations of cyclic peptides, aiming to accelerate the drug discovery process.
A peptide is a short chain of amino acids linked together by peptide bonds, typically containing about 2-50 amino acid residues. A cyclic peptide is a peptide that forms a circular structure. While cyclic peptide drugs offer compelling advantages over traditional small molecules [1, 2], running docking simulations for them with an external protein is both time consuming and error prone due to a higher number of rotatable bonds.
In this blog post, we summarize the efforts that AWS took in collaboration with Chugai to formulate the cyclic peptide docking problem in the quantum-amenable quadratic unconstrained binary optimization (QUBO) formalism. Modeling the problem as a QUBO enables the application of both classical and quantum optimization approaches, such as classical and quantum annealing, to optimize the placement of peptide particles. We also develop a Constraint Programming (CP) model that we use as a baseline approach. We test our methods on example instances taken from the Protein Data Bank (PDB) and use our end-to-end framework to predict the three-dimensional structure of various cyclic peptides in the presence of an external protein. While both approaches successfully predicted conformations, the QUBO-based approach faced scaling limitations beyond six peptides and 34 protein residues, whereas the CP approach was able to solve all of the instances in our test set.
For more details, see our scientific paper published in Scientific Reports.
Representation of cyclic peptide and external protein
To represent the peptide at hand, we use the so-called “coarse grained” representation for each amino acid, where the main and side chain atoms are represented as single particles. We use two particles for all amino acids except for Glycine, which has no side chain and thus needs only one particle (Figure 1).
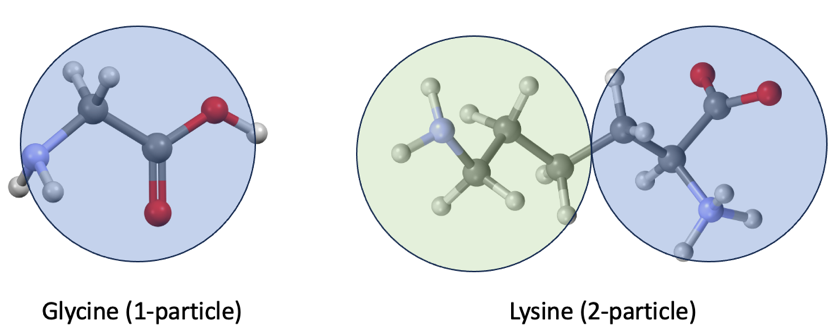
Figure 1 – Example coarse grained representation of Glycine (G) with 1-particle and Lysine (K) with 2-particles. Blue is used for the main chain, and green for the side chain.
We place these peptide particles on a three-dimensional tetrahedral lattice, for instance as depicted in Figure 2. Interaction between residues is calculated using Miyazawa-Jernigan (MJ) potentials [3]. The goal is to find the optimal placement of particles on the lattice that minimizes the total interaction energy while satisfying cyclization conditions and ensuring particles do not overlap.
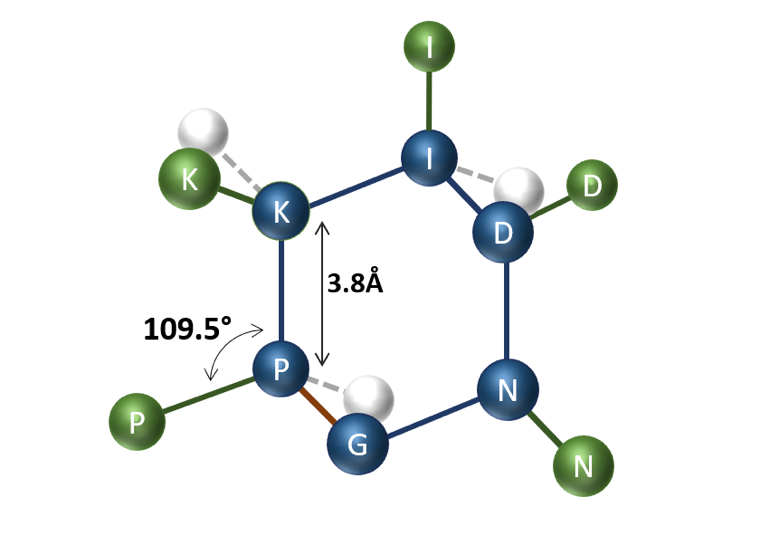
Figure 2 – Possible arrangement of cyclic peptide P-K-I-D-N-G on the tetrahedral lattice with blue representing the main chain and green the side chain. The cyclization bond is highlighted in red. Some of the unoccupied vertices of the tetrahedral lattice are illustrated in white.
We consider only the “active site” of the target protein, a focused area that the peptide is likely to use for docking. This reduces the problem space and improves the likelihood of finding the optimal orientation of the peptide. To identify the active site in a target protein, we locate the residues that are within a specified distance (in this case, 5Å) from the peptide residues. The protein affects the peptide on the grid in two ways: it blocks some spots that are too close (within 3.8Å) where the peptide can’t fit, and it creates interaction zones (within 6.5Å) where the protein and peptide can interact. After removing the blocked spots, we calculate the energy between each peptide part and nearby protein parts at interaction spots. The distances we choose for the active site, blocked areas, and interaction zones affect what solution the system finds.
QUBO model
We explore modeling and solving this problem with the quantum-amenable quadratic unconstrained binary optimization (QUBO) formalism. QUBO is a combinatorial optimization problem that seeks to minimize a quadratic function involving binary (0 or 1) variables. In our work, we start by expressing the problem as a higher-order binary optimization problem and then use locality reduction techniques to transform it into a QUBO.
Various Hamiltonian formulations of the protein folding problem without docking with different encoding strategies have been previously introduced and analyzed. Early work by Perdomo et al. [4] used a spatial encoding to map protein positions to a 2D grid. Researchers then developed a turn encoding [5], which describes protein shape through a series of turns, making it more efficient for longer proteins. Several teams improved this method: Babbush et al. [5] created the “turn ancilla” approach, while others adapted it for different lattice types and quantum computing methods.
Our formulation is an extension of the “resource efficient” turn encoding method [6]. The initial model includes interpeptide interactions, non-sequential particle overlapping constraints and imposes no-backtracking constraints to prevent sequential particles from overlapping. Thus, the formulation is composed of two parts: Hcomb, which handles interpeptide interactions and no-overlap penalties, and Hback, which ensures subsequent particles do not backtrack to the same lattice point. To extend this model, to incorporate the external protein for cyclic peptides, two additional terms are introduced: Hcycle for enforcing peptide cyclization and Hprotein for peptide-protein interactions and steric clashes.
The Hcycle term enforces cyclization between specific residue pairs by ensuring that they are 1-NN (nearest neighbor) on the lattice, using a distance function d(x,y) that calculates the lattice steps between vertices. For peptide-protein interaction, Hprotein includes MJ interaction energies for peptide residues within the protein’s interaction range and a penalty for steric hindrance on blocked sites.
The final formulation combines all these terms extending the original model to include cyclization and protein interaction considerations.
H = Hcomb + Hback + Hcycle + Hprotein
- Hcomb: Combines interpeptide interaction energy with no-overlap constraint penalties
- Hback: Enforces no-backtracking constraints for sequential particles
- Hcycle: Implements the cyclization constraint
- Hprotein: Handles peptide-protein interactions and steric clashes
CP model
As a baseline, we develop a Constraint Programming (CP) model for the problem. CP is a paradigm for solving constraint satisfaction and optimization problems that involves both a problem model, and a backtracking search-based solver. Typically, users describe their problem using specific variables and constraints, and then the search is done to find the solution by trying different possibilities. The term “programming” here refers to planning rather than computer coding.
Key constraints enforced in the CP model:
- Placement of residues on valid lattice points, excluding positions affected by external protein steric hindrance
- Maintaining correct distances between bonded residues
- Preventing overlaps between residues
- Enforcing cyclization bonds
The objective function minimizes the total MJ interaction energies of adjacent particles. The CP model is designed to minimize interaction energies between residues on a lattice while adhering to various spatial constraints. It uses the flexibility of CP to handle logical constraints and non-linear relationships that are difficult to manage in linear programming models. The model ensures that residues are placed correctly on the lattice, avoids overlaps, and considers interactions within a defined threshold.
Results
To evaluate our approaches, we developed an end-to-end pipeline for processing protein-peptide complexes from the Protein Data Bank (PDB) and predict the optimal three-dimensional structure of the docked peptide. The PDB repository contains detailed, standardized atomic-level coordinates for cyclic protein complexes. The pipeline involves the following steps, as shown in Figure 3:
- The PDB file is divided into two parts: the peptide and the target protein.
- The protein active site, a smaller, focused area where the peptide is likely to dock, is identified.
- Each atom within the peptide is categorized as part of the main chain or side chain, and the weighted centroids of these groups are calculated, resulting in a 2-particle representation for each amino acid in each structure.
- A tetrahedral lattice is generated to discretize the search space for discrete optimization approaches.
- The lattice is filtered based on the active site coordinates and a steric clash radius to remove vertices that would clash with the target site, resulting in the final lattice structure.
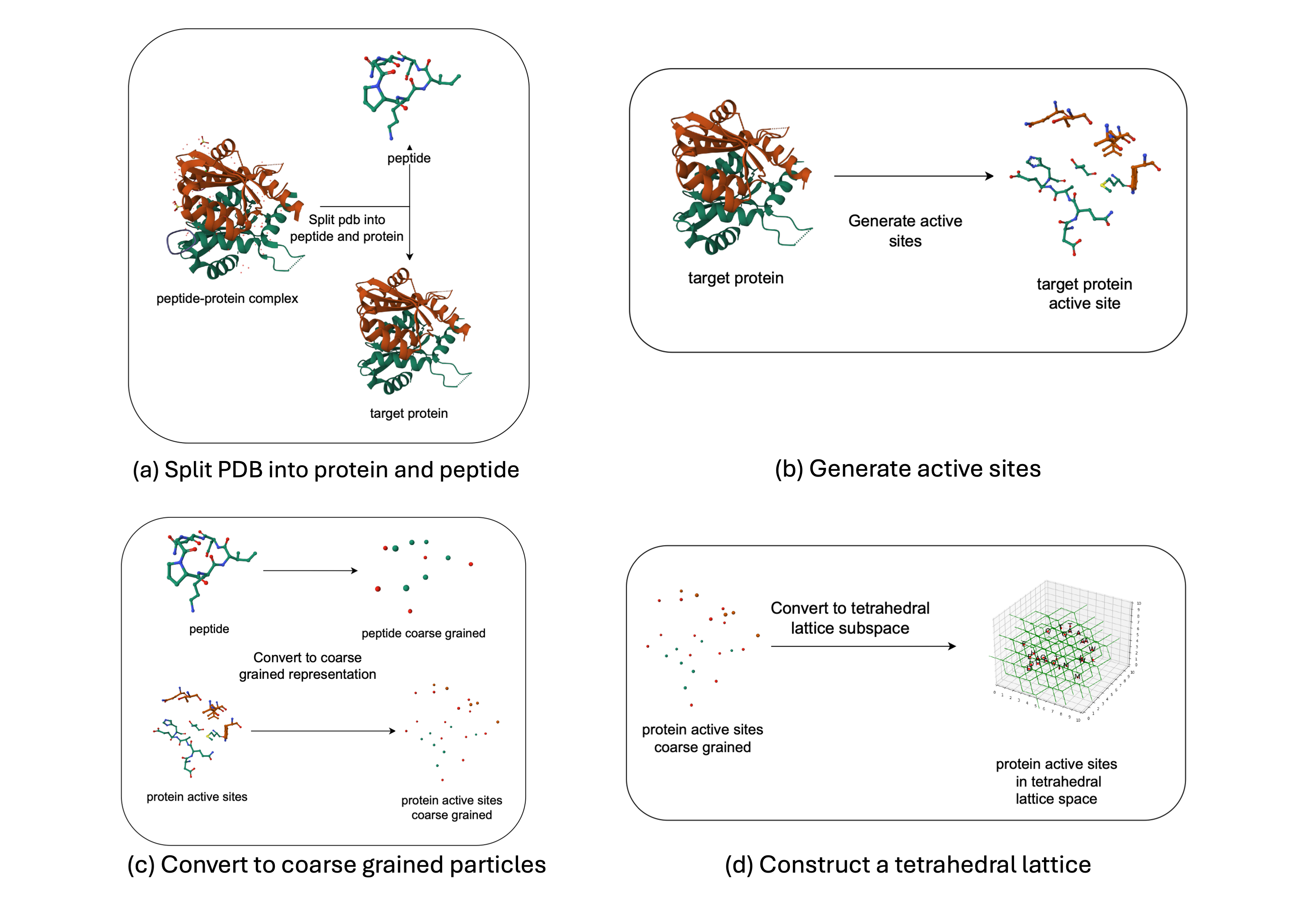
Figure 3 – Conversion from atomic level representation to 2-particle coarse grained tetrahedral representation.
The PDB serves as a ground truth which we can measure our predictions against. However, the tetrahedral lattice has its drawbacks. Real peptides aren’t fixed to rigid structures; rather natural forces determine their shape and form. Thus, it’s difficult to compare the model’s predicted and actual protein structure from the PBD. Nonetheless, we assessed the solutions produced by our approach in terms of both their MJ interaction value and the root mean square distance (RMSD) when compared with the coordinates of the real peptide (sourced from the PDB file) in Euclidean space. The RMSD measures the average distance between the coarse-grained particles of the real (PDB) peptide and the peptide structure produced by our approach. Any RMSD value above 4Å is considered too inaccurate for practical use
| PDB ID | Peptide Chain | Number of Residues | |
|---|---|---|---|
| Peptide | External Protein | ||
| 3WNE | P-K-I-D-N-G | 6 | 26 |
| 5LSO | K-S-R-W-D-E | 6 | 34 |
| 3AV9 | S-A-K-I-D-N-L-D | 8 | 28 |
| 3AVI | S-L-K-I-D-N-M-D | 8 | 32 |
| 3AVN | S-H-K-I-D-N-L-D | 8 | 28 |
| 2F58 | H-I-G-P-G-R-A-F-G-G-G | 11 | 49 |
Table 1: RCSB Protein Databank (https://www.rcsb.org/ ) peptide-protein complexes used for our experimental analysis.
We analyzed six peptide-protein complexes from the PDB, ranging from 6 to 11 residues in the peptide and 26 to 49 residues in the protein active site, as shown in Table 1. For the QUBO model, we applied simulated annealing, a heuristic solver approach, implemented using an open-source python hybrid framework. We performed hyperparameter optimization using Bayesian optimization via Amazon SageMaker. The CP model was implemented using the OR-Tools library and solved to optimality with a 300-second time limit on Amazon EC2 m5.4xlarge instances.
| PDB ID | Without External Protein | With External Protein | ||||||
|---|---|---|---|---|---|---|---|---|
| MJ potential | RMSD (Å) | MJ potential | RMSD (Å) | |||||
| QUBO | CP | QUBO | CP | QUBO | CP | QUBO | CP | |
| 3WNE | -1.87 | -1.87 | 10.03 | 7.77 | -28.53 | -42.64 | 8.88 | 8.48 |
| 5LSO | -5.93 | -5.97 | 13.31 | 13.20 | -17.93 | -23.26 | 7.68 | 10.29 |
| 3AV9 | -6.18 | -6.64 | 11.36 | 9.92 | – | -40.44 | – | 8.98 |
| 3AVI | -7.43 | -8.34 | 9.65 | 9.39 | – | -62.34 | – | 8.74 |
| 3AVN | -6.52 | -6.88 | 10.60 | 10.75 | – | -55.12 | – | 8.34 |
| 2F58 | -6.18 | -13.61 | 11.52 | 11.39 | – | -4.02 | – | 10.42 |
Table 2: With and without external protein MJ interaction and RMSD values for QUBO approach vs CP approach.
Table 2 compares the performance metrics (MJ potential and RMSD) between the QUBO and CP approaches for each peptide, with and without external protein, as there is no benchmark from previous studies to compare our results against. The QUBO approach was able to find feasible solutions for problems with up to six peptide residues and 34 target protein residues. A feasible conformation/solution is a conformation that satisfies all problem constraints but may have suboptimal MJ interaction potential. However, it struggled with larger instances, often producing solutions that violated problem constraints. This occurs because in the QUBO model, constraints must be incorporated into the objective function through penalty terms. Without the protein present, the QUBO method successfully solved all test cases, finding the lowest energy scores in five out of six cases, with only 2F58 performing worse than the CP method. Both methods showed comparable accuracy (RMSD) in matching real structures. However, when including the protein, QUBO only worked for two out of five peptides (3WNE and 5LSO), and achieved higher energy scores than CP in both cases. The QUBO showed even higher accuracy for 5LSO based on RMSD. Figure 3 demonstrates how both QUBO and CP methods successfully modeled peptide 5LSO with the protein present, producing valid structures when compared to the actual protein database structure. This suggests that optimizing for energy scores doesn’t always lead to more accurate structure predictions, especially when starting from suboptimal positions on a tetrahedral lattice model. The CP approach demonstrated scalability, solving problems with up to 11 peptide residues and 49 target protein residues to optimality.
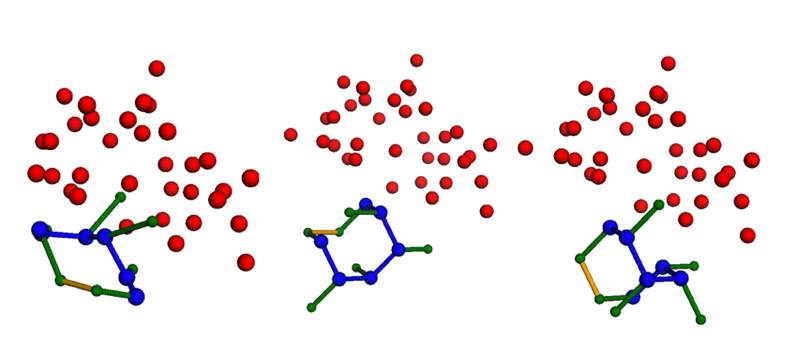
Figure 4 – 5LSO result visualization. Comparing the true PDB peptide (left) against the QUBO model result (middle) and the CP-MJ 1-NN result (right). The peptide is represented with blue and green dots (main and side-chain, respectively), and the red dots are the external protein residues.
Conclusion
In this post, we introduced a quantum-amenable binary formulation for the cyclic peptide docking problem. QUBO and CP approaches were compared across a set of peptide instances, with QUBO finding feasible solutions for smaller problems (up to six peptide and 34 protein residues) with competitive MJ interaction energy, while CP demonstrated better scalability by solving larger problems (up to 11 peptide residues and 49 target protein residues) to optimality, as illustrated in the case of peptide 5LSO.
The QUBO approach performed well in protein-free environments, nearly matching CP results in solution quality. However, its struggle with feasibility in protein-present scenarios, combined with the inherent challenges of representing distance-dependent interactions in the formulation, suggests that quantum optimization techniques based on QUBO formulations may not be the best path forward for this specific application. While the current QUBO approach has limitations, particularly in scalability, it provides a foundation for future work as both algorithms and quantum hardware evolve.
The performance of the CP approach also highlights the continuing relevance of traditional optimization methods in computational biology. As the field progresses, hybrid approaches combining quantum and classical techniques may prove most effective in tackling complex biomolecular modeling problems. Looking ahead, the robust performance and scalability of the CP approach positions it as a more promising avenue for future development in peptide-protein interaction studies. These findings not only contribute to our understanding of computational protein modeling but also provide valuable guidance for researchers in choosing appropriate methodologies for similar biological optimization problems.
The use of a lattice structure to model cyclic peptide docking, while simplifying the problem, introduces inherent limitations since real peptides aren’t constrained to rigid structures but rather follow natural steric forces. This simplification contributes to the significant RMSD (Root Mean Square Deviation) values observed in the results when comparing the model predictions to actual PDB (Protein Data Bank) structures.
For those interested in peptide drug design or computational structural biology, this work offers valuable insights into current algorithmic approaches and their tradeoffs. It also underscores the importance of continued research to bridge the gap between simplified computational models and the complex reality of biomolecular interactions. You can read our paper on Scientific Reports for a more detailed discussion about the methods, implementation approach, and end-to-end pipeline. For assistance with similar challenges, contact AWS to learn how AWS Professional Services and the Amazon Quantum Solutions Lab can support your needs.
References
[1] L. Wang, N. Wang, W. Zhang, X. Cheng, Z. Yan, G. Shao, X. Wang, R. Wang, C. Fu, “Therapeutic peptides: current applications and future directions”. In Signal Transduction and Targeted Therapy 7 (1) (2022).
[2] A. Ohta, et al., “Validation of a New Methodology to Create Oral Drugs beyond the Rule of 5 for Intracellular Tough Target”. J. Am. Chem. Soc 145 (44) (2023).
[3] S. Miyazawa, R. Jernigan, Estimation of effective interresidue contact energies from protein crystal structures: quasi-chemical approximation, Macromolecules 18 (3) (1985)
[4] A. Perdomo, C. Truncik, I. Tubert-Brohman, G. Rose, A. Aspuru-Guzik, Construction of model hamiltonians for adiabatic quantum computation and its application to finding low-energy conformations of lattice protein models, Physical Review A 78 (012320)
[5] R. Babbush, A. Perdomo-Ortiz, B. O’Gorman, W. Macready, A. Aspuru-Guzik, Construction of energy functions for lattice heteropolymer models: Efficient encodings for constraint satisfaction programming and quantum annealing, Advances in Chemical Physics, John Wiley & Sons, Inc., 2014, pp. 201–244.
[6] A. Robert, P. K. Barkoutsos, S. Woerner, I. Tavernelli, “Resource-efficient quantum algorithm for protein folding”, npj Quantum Information 7 (38)