AWS HPC Blog
Simulating 44-Qubit quantum circuits using AWS ParallelCluster
Dr. Fabio Baruffa, Sr. HPC & QC Solutions Architect
Dr. Pavel Lougovski, Pr. QC Research Scientist
Tyson Jones, Doctoral researcher, University of Oxford
Introduction
Currently, an enormous effort is underway to develop quantum computing hardware capable of scaling to hundreds, thousands, and even millions of physical (non-error-corrected) qubits. Ultimately, this is to build fault-tolerant quantum computers. Classically simulating the behavior of systems with a large number of qubits is a key to understanding the behavior of physical quantum systems under varying noise conditions as they scale.
Simulations are also invaluable to understand the noise resilience of quantum algorithms. Because the noise characteristics of today’s hardware prototypes often defy analytic treatment, they are instead investigated through small-scale experiments and intensive numerical modelling. Even performance evaluations of perfect noise-free quantum algorithms typically require some form of classical emulation.
Unsurprisingly, such emulation tasks are computationally demanding and memory intensive, so the researchers must use high performance computing (HPC) strategies like data and algorithm distribution when modelling even modestly-sized present-day quantum experiments. HPC simulators of quantum computers are therefore an indispensable tool in the advancement of experimental and algorithmic research.
In this blog post, we describe how to perform large-scale quantum circuits simulations using AWS ParallelCluster with QuEST, the Quantum Exact Simulation Toolkit. We demonstrate a simple and rapid deployment of computational resources up to 4,096 compute instances to simulate random quantum circuits with up to 44 qubits.
Prerequisites
Quantum computing has the potential to accelerate current computation capabilities using the principles of quantum physics, and possibly solve specific complex problems that are difficult to address with conventional computers. This is a major area of research field, where new hardware and software needs to be developed. Currently, a crucial role is played by classical simulations of quantum computers for demonstrating and proofing new ideas and experimenting before a production environment is developed.
Classic simulations
Quantum computers can be classically simulated using a variety of algorithmic paradigms, each with their own costs and performance trade-offs. The choice of the simulation algorithm is often determined by the nature of the questions asked about the emulated quantum device, such as the probability of a particular error occurring, or the expected value of an observable. We will introduce two ubiquitous paradigms: state-vector (SV) and tensor-network (TN) simulation.
SV simulators, also known as “full-state”, “brute-force” and “Schrödinger-style” simulators, maintain a complete numerical description of the evolving quantum state of a quantum circuit. As such, they require memory that scales exponentially with the number of qubits in the circuit, but their runtime scales linearly with the quantum circuit depth. Since their complete quantum state output permits the precise and efficient a posteriori calculation of any property, they are the conventional first choice of simulator for much of quantum computing research.
In contrast, TN simulators have constant growing memory requirements as the number of qubits increases. TN simulators are exponentially slowed by deepening circuits and increasing state complexity. This makes them cheaper and faster in the study of shallow circuits with a suitable structure, and the simulation can potentially scale to many qubits.
The performance bottleneck of SV simulators is the propagation of a quantum state, while for TN simulators, it is the propagation of a particular observable. QuEST is a SV simulator and in this blog post, we will employ it for the study of circuits for which SV simulation is particularly well suited
In a State-vector (SV) simulation, an N-qubit register is represented by a state-vector of 2N complex amplitudes and can be numerically instantiated as an array of 2×2N real floating-point numbers. SV simulation of N=40 qubits at double precision would therefore require 16,384 GiB, well beyond the capacity of a typical HPC compute node. This makes the use of distributed memory systems essential. To date, large-scale SV simulations were performed exclusively on purpose-built supercomputers and required a long lead time just to allocate the resources.
AWS resources
If you are interested in simulating small to moderately-sized quantum circuits, Amazon Braket offers the choice of several simulators. These include the local simulator that is included in the Braket SDK and three on-demand simulators. The local simulator can run on a laptop or within an Braket managed notebook and supports simulation of quantum circuits with and without noise
The on-demand simulators are SV1, a general-purpose state vector simulator; DM1, a density matrix simulator that supports noise modeling; and TN1, a tensor network simulator that specializes in certain larger scale structured quantum circuits. SV1 is suitable for circuits up to 34 qubits, and DM1 supports the simulation of circuits up to 17 qubits. While TN1 can simulate up to 50 qubits, it can be used only for suitably structured quantum circuits. This blog complements the Braket simulators by exploring the scalability of larger SV simulation circuits with up to 44 qubits using the QuEST simulator on Amazon Elastic Compute Cloud (Amazon EC2).
Amazon EC2 provides a wide selection of instance types optimized to fit different use cases. Amazon EC2 compute-optimized instances are ideal for compute bound workloads and intensive numerical modeling. For example, 256 c5.18xlarge (144 GiB of memory) instances would together contain sufficient memory to store the distributed state-vector for a 40-qubit circuit, including the doubled memory costs of storing the necessary auxiliary buffers for MPI communication. Of course, simulating just an additional qubit will double the total memory requirement. Simulation of an N=44 qubit register requires 562,950 GiB (~0.5 PiB) of memory or 4,096 c5.18xlarge instances.
To orchestrate your compute resources, AWS developed an open-source cluster management tool, AWS ParallelCluster, which simplifies deploying and managing HPC clusters on AWS. AWS ParallelCluster enables the rapid deployment of virtual clusters with varying architectures to meet the requirements of different applications and workflows. You can also run your computation immediately when needed without waiting in a queue for a shared compute resource. As a result, many scientists and companies worldwide are looking to use cloud computing to find solutions to their problems in an efficient and cost-effective manner.
The remainder of this blog post demonstrates an HPC deployment of QuEST with AWS ParallelCluster to simulate random circuits. Random circuits appear both in the verification of real quantum computers and in the performance benchmarking of quantum computing simulations.
Circuit Details
We use QuEST to simulate a generic quantum circuit in a distributed memory system. We sample the probability distribution over N-bit strings produced by N-qubit circuits using one- and two-qubit gates and multi-qubit controlled gates. We implemented a set of random N-qubit quantum circuit using the following algorithm:
- Set the total number of qubits N and gates Gn in a circuit
- Looping for each gate in Gn:
- toss an unbiased coin
- if the outcome of the coin toss is heads:
- choose two indices (q1, q2) randomly, each from 1 to N
- apply two-qubit CZ gate between qubits q1 and q2
- if the outcome of the coin toss is tails:
- choose an index q1 randomly from 1 to N
- choose a single qubit gate G from {RX, RY, RZ, H} uniformly at random
- if G is H:
- apply H to qubit q1
- if G is RX, RY, or RZ
- choose a random number θ between 0 and pi (3.1415…)
- apply the corresponding rotation by the angle θ to the qubit q1
The single qubit gates RX, RY, RZ are the rotation gate along the respectively axis and the H is the Hadamard gate. The two-qubit gate CZ is the controlled phase flip.
The randomness of the circuits prevents particular symmetries being explored to optimize the classical simulation.
We run circuit simulations in QuEST by iterating over the number of qubits, starting from N=40 to N=44 and using the following number of gates Gn=(100, 200, 400, 600, 800, 1000) for each value of N. We always initialize the quantum state of the circuit to ∣0⟩⊗N and compute 2N complex amplitudes of the final state after the random circuit is applied to the initial state. Because SV simulations are implemented as a sequence of Gn matrix-vector multiplications, we estimate the total number of floating-point operations (FLOP) complexity of simulating a single complex amplitude in the final state vector by recording the number of elementary multiplication and addition operations and dividing them by the total number of amplitudes (2N).
Circuit Complexity
The computational complexity of simulating a random N-qubit circuit using an SV simulator, such as QuEST, grows exponentially with N but scales linearly with the number of single- and two-bit gates Gn. In other words, the computational cost does not discriminate between different circuit structures.
Other simulation approaches, such as tensor network (TN) simulations, are much more sensitive to random circuit structure. TN simulators do not compute an entire N-qubit state vector but rather can find an optimal contraction path for estimating a single amplitude in the state vector. Many amplitudes in a state vector generated by a random circuit can be 0 and do not need to be evaluated explicitly and TN simulators can help identify amplitudes for which this holds.
However, random circuits with circuit depth greater than 400 gates incur a large computational cost per amplitude that grows polynomially with the circuit depth. These circuits are better suited for SV simulations where simulation cost grows linearly with the depth.
Resources deployment
We demonstrate large-scale simulations of quantum circuits using QuEST, an open-source quantum state vector simulator. QuEST can run multithread and distributed calculations using MPI/OpenMP to accelerate simulations on HPC systems. The HPC infrastructure is deployed using AWS ParallelCluster. The following diagram shows the HPC architecture.
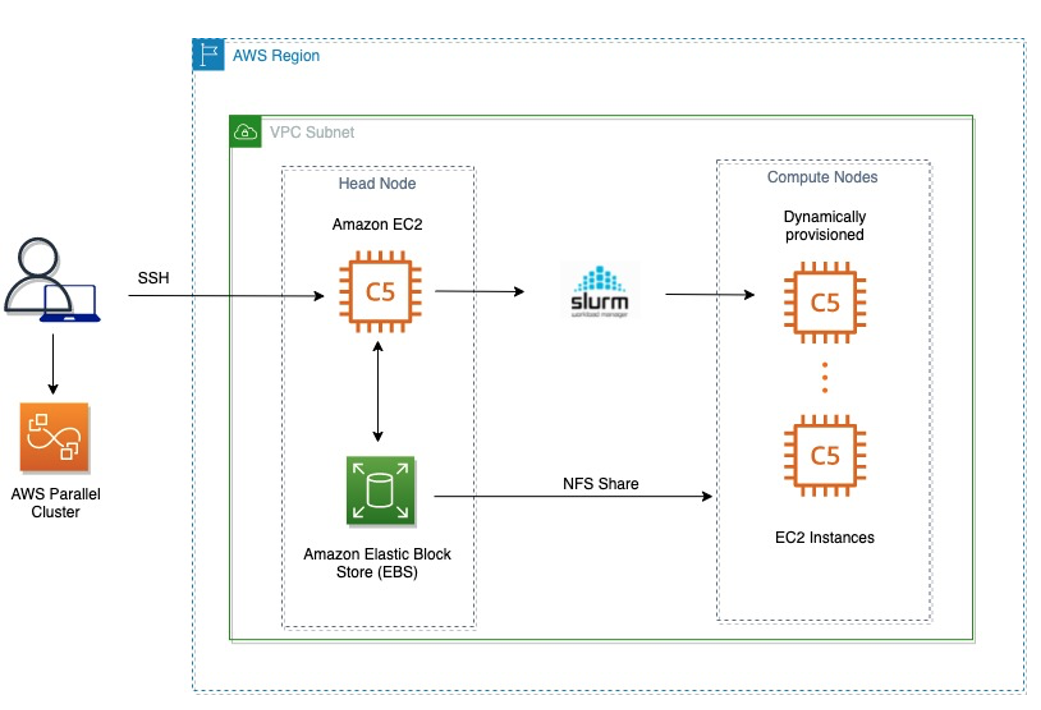
Figure 1: HPC Architecture
The Head Node is used to log in to the cluster, compile the application, submit the job, and set up Compute Nodes, which are dynamically provisioned according to the size of the problem (number of qubits).
We use the EC2 c5.18xlarge compute-optimized instances with Intel Xeon Scalable Processors with a sustained all core Turbo frequency of 3.4GHz. The instances are equipped with 36 cores and 144 GiB of memory per node, which gives the best compromise between resources required for the circuit and performance. The memory-per-core ratio is 4 GiB, which allows for an efficient usage of 2 MPI tasks per instance. The following table shows the required resources for simulations with 36 to 44 qubits.
| Number of qubits | Memory Required (GiB) | Number of instances | Total available memory EC2 (GiB) | Total number of cores |
| 36 | 2,199 | 16 | 2,304 | 576 |
| 37 | 4,398 | 32 | 4,608 | 1152 |
| 38 | 8,796 | 64 | 9,216 | 2,304 |
| 39 | 17,592 | 128 | 18,432 | 4,608 |
| 40 | 35,184 | 256 | 36,864 | 9,216 |
| 41 | 70,369 | 512 | 73,728 | 18,432 |
| 42 | 140,737 | 1,024 | 147,456 | 36,864 |
| 43 | 281,475 | 2,048 | 294,912 | 73,728 |
| 44 | 562,950 | 4,096 | 589,824 | 147,456 |
Table 1: Resources required by the state vector simulator to simulate a circuit with the given number of qubits.
We compiled QuEST version 3.5.0 from source code with the Intel OneAPI HPC toolkit, version 2022.2, to take advantage of the performance optimization provided by the AVX512 and AVX2 vector instructions available on C5 instances. We used Amazon Linux 2 for the operating system, and the Intel OneAPI MPI 2022.2 for the network library.
Performance results
We explore the scalability of the simulation with respect to the number of instances. Adding one additional qubit doubles the memory requirements and the number of instances required by the state vector simulator. In all experiments, we use 2 MPI tasks per instance with 18 OMP threads, and we disable hyperthreading.
Figure 2 plots the time to simulate the quantum random circuit as a function of the circuit depth.
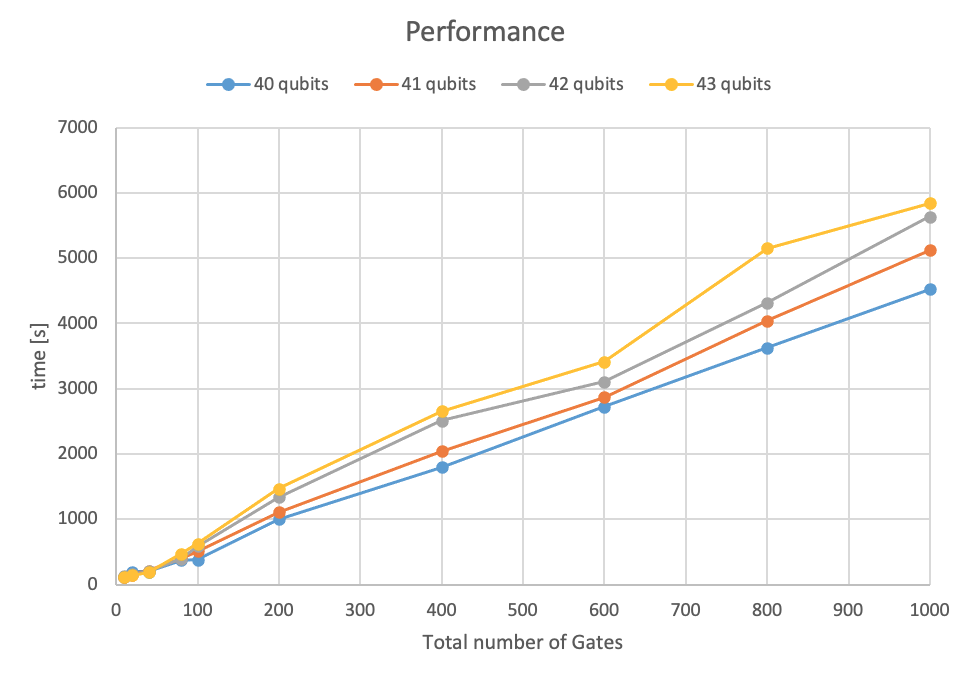
Figure 2: Simulation time as a function of circuit gate depth for circuits with different number of qubits.
For a fixed number of qubits, the execution time scales close to linearly with the number of gates. It demonstrates that QuEST has a predictable behavior when running on larger and complex circuits.
Figures 3 and 4 show the performance of the simulation as a function of the number of qubits in the circuit and with a fixed circuit gate depth.
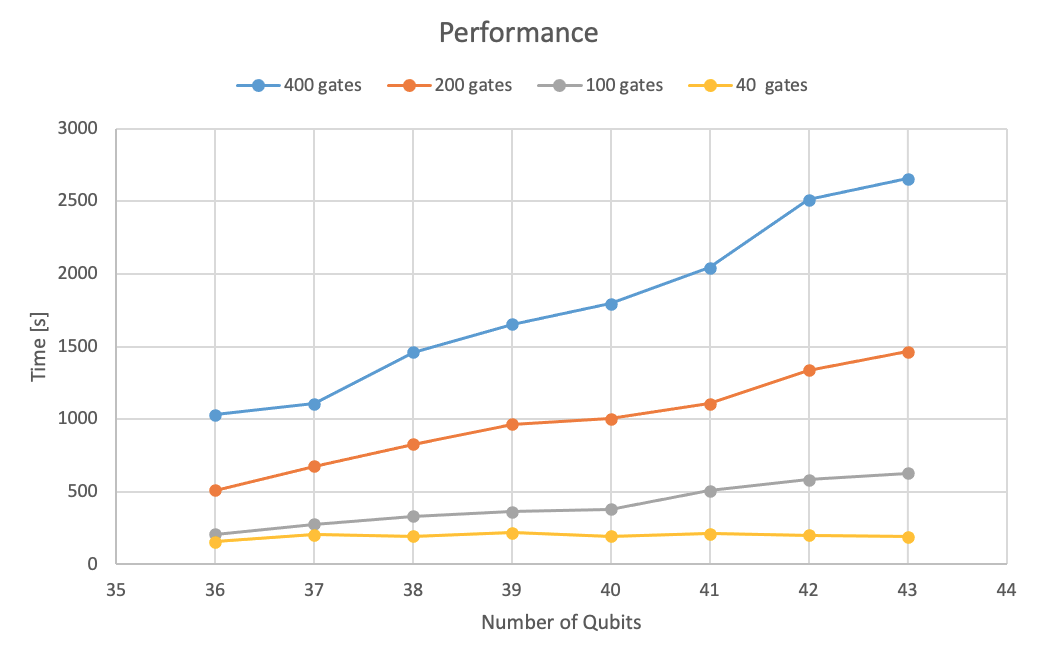
Figure 3: Simulation time as a function of the number of qubits for small circuit gate depths.
For small depth circuits, increasing the number of qubits by 1 unit, the computational resources doubles, but the completion time remains constant, showing a weak scaling behavior of the simulation. This behavior can be observed for circuits up to 100 or in a small variation also to 200 gates. For more complex circuits, with gate depth greater than 200, the application scales linearly with the number of qubits and the simulation time increases. This is due to the increasing amount of distributed data among the processes that needs to be exchange to perform the computation. In this regime, the problem is communication bound.
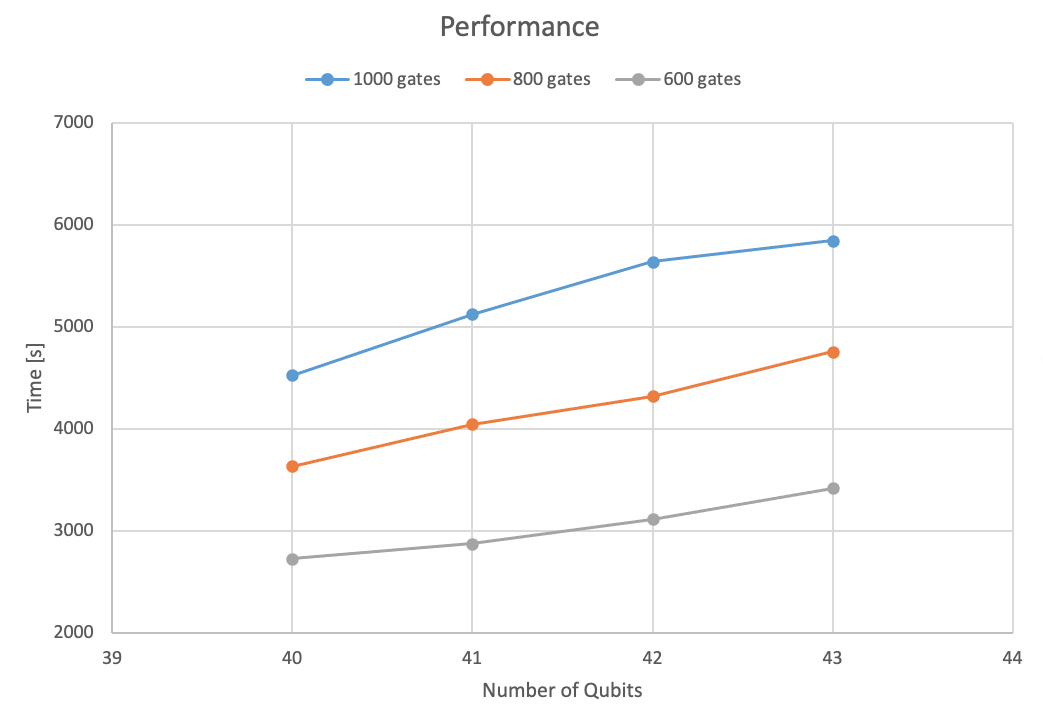
Figure 4: Simulation time as a function of the number of qubits for large circuit gate depths.
Conclusion
We performed large-scale, high-performance quantum circuit simulations using the open-source quantum state vector simulator QuEST on HPC cloud recourses, demonstrating the scalability of the simulator and the AWS platform.
The on-demand acquisition and deployment of the required computational resources using AWS ParallelCluster illustrates how a tightly coupled workload can be made readily available for scientific simulation.
Our study also confirms that the AWS infrastructure for cloud computing is well-suited to the emulation and study of present-day quantum computers. We were able to allocate as many as 4096 EC2 instances of c5.18xlarge to simulate a non-trivial 44 qubit quantum circuit in fewer than 3.5 hours.