Supply chain network optimization – cutting through complexity to maximize efficiency

Unpredictable events such as the global pandemic, Brexit, the Suez Canal, and Ukraine highlight the importance for robust, stress-tested, and agile supply chain (SC) networks. Such large scale and disruptive events level the field and affect all industry players. Consequently, businesses that are quicker and more efficient to adapt to new circumstances gain market share and a competitive advantage. With rising inflation, customers are becoming more sensitive to pricing, product availability, and delivery speed. Supply chain executives need to consider such recent developments, which sometimes have business altering implications. However, making end-to-end supply chain decisions is not a straightforward task given the complexity we observe in networks (e.g., a large number of suppliers, complex manufacturing processes, long delivery routes from Asia to Americas and Europe, large variability of inbound and outbound delivery options, distributed storage networks, and a variety of distribution channels). The list of supply chain challenges is long, diverse, and keeps growing. This is where supply chain network optimization helps support holistic decision making. Despite an abundance of theory on the topic, when it comes to practical examples of dealing with complex supply chain networks, there is less guidance and experience sharing. In this blog post, we will demonstrate an approach, which proves itself useful when dealing with highly complex networks (i.e., billions of granular decisions that all contribute to a handful of bottom line numbers in quarterly business reports).

Executive discussion – our layering approach to network optimization

Executives are starting to challenge their supply chains and Data Scientists with the following questions: How can we analyze our supply chain end-to-end? How can we find the best overall decision instead of several optimal ones for each department? How can we accommodate more operational details into our network modelling (e.g., schedules, transport units, order volumes by hour, manufacturing batches, and more)? Such a holistic approach considers all plants, ports, distribution centers, warehouses, and points of sale simultaneously while considering their interactions with processes, technology, and the organization. In addition, uncertainties inherent in supply chains, whether external or internal, add further complexity to holistic network optimization.

Previously, network optimization commonly supported large structural business changes. For example, mergers to derive a consolidated optimal footprint of an enlarged company, find excess or shortages of capacity, and introduce connections between previously unrelated sites. However, we observe modern uses of network optimization that are more diverse than merger and acquisition activity alone, and the method is now finding new, regular, and repeatable applications. Non-exhaustive examples include: (1) footprint assessments to find best locations for new production, storage or cross-docking sites, or to decide which sites to consolidate or shut down; (2) operational support decisions and master planning (e.g., seasonal capacity preparations, how much and where to produce and store, decisions on product from-to flow, and transport scheduling that impacts network flows); (3) network stress testing (e.g., for rapid demand growth, breaks in supply, and intermittent production to understand their implications and derive contingency plans); (4) continuous improvements and incremental network changes (e.g., assessing implications of quicker transit times for certain connections, later cut-offs for next day delivery, and different transport modes); (5) unconstrained capacity networks to highlight main differences compared to the current state, and provide valuable inputs for future growth strategy.

The traditional way to approach network optimization is to follow the supply chain organizational structure and break the modelling down into sequential value-adding stages (e.g., inbound flows, manufacturing, storage, outbound, etc.) and attempt to include all or most of the operational complexities in each stage. While this closely mimics the given organizational structure and decision making process, it typically has two challenges:

(1) It often results in imbalances between modelled network stages in terms of computational effort to solve an optimization for the corresponding decision. For example, outbound distribution may be more complex than inbound flows or the other way around. Some organizations end up with models that may take days to solve and not necessarily to the proven optimality. A typical first reaction is to use brute force by throwing in more computational power, which may not work;

(2) There is typically limited coupling between sequential network models following the organization (e.g., outbound distribution simply consumes manufacturing outputs as inputs with limited or no scenarios of what could be a better decision for both functions).

Our recommended approach follows hierarchical layering and addresses both challenges by introducing solution layers based on covered supply chain scope, decision horizons, and uncertainty. For example, as a starting point, we recommend creating an overarching supply chain network model that deals with longer time horizons (e.g., a year or more) and aggregates uncertainty on higher levels (e.g., dealing with a few product families rather than individual SKUs, site clusters, flow corridors, etc.). This reduces the complexity and limits computational effort to a degree but addresses the challenge of modelling a supply chain network end-to-end and sets an overall strategy. The subsequent layers add more details and involved uncertainty but also reduce the modelled network scope. The illustration below is an example of a hierarchically layered approach with a balanced complexity decomposition.

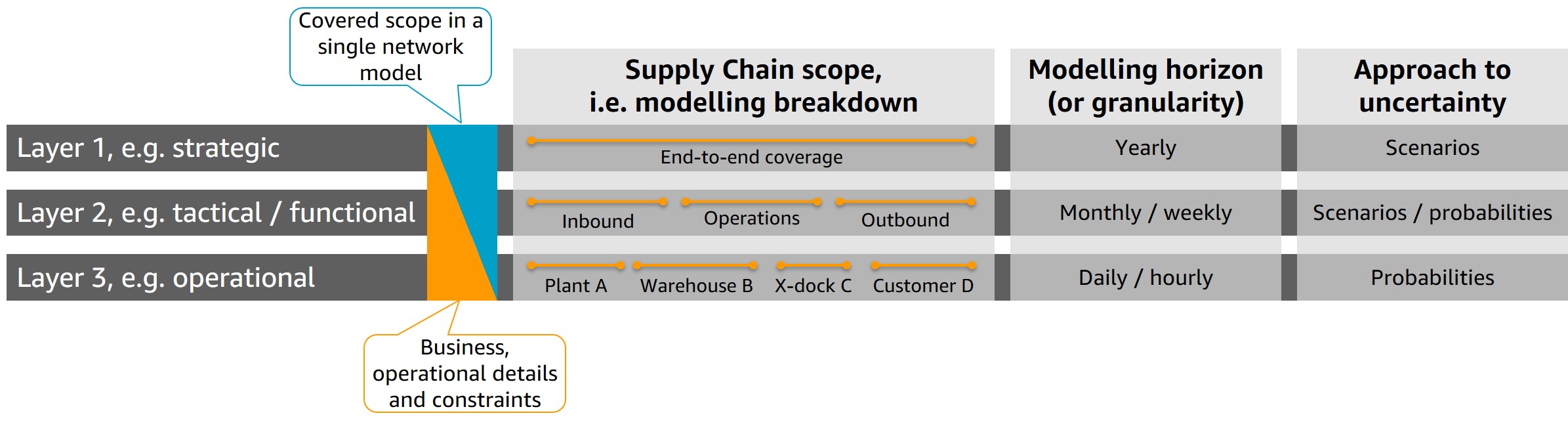
The essence of layering the network optimizations while maintaining a balance between the layers with respect to their computational challenges is based on both:

• the timing aspect of decision making (i.e., longer planning horizons come before shorter ones)
• the level of uncertainty (i.e., focusing on aggregated and more deterministic data before considering uncertainties)

This approach aligns the computational (mathematical) challenge of the problems to solve at each layer. The problems looking at longer planning horizons with less uncertainty are at larger scale and their complexity stems from the scale or scope of the problem. The problems dealing with shorter planning horizons with a higher level of uncertainties may be smaller at scale but require more sophisticated methods to handle the uncertainty (e.g., by including statistical distributions). As a result, the layered approach balances the mathematical complexity and the computational efforts across the layers and alleviates the challenge of solution speed and quality we previously discussed. Furthermore, the approach also alleviates the challenge of “sum of local optimums” by solving the problem first for the longer time horizon and aggregated data, which can be used as a guiding North Star for the subsequent layers (e.g., by establishing optimal interactions between functions). Naturally there will be some benefit loss on the lower layers versus the global optimum but at least the higher layers set the target for the interoperation between functions.

With the balanced layering approach, there is no single recommendation on how to break down the network optimization process into layers. It depends on the size of the network, sources of complexity, types of products and services, degree of freedom existing in the business, etc. For example, a regional logistics company may have two layers: a high level to determine locations of the local depots, cross-docks, aggregated flow paths, capacity, etc. and a lower level to decide on dock scheduling, daily volumes, and the last mile delivery routing as individual models for focused decision making. Whereas a large pan-EU or a national US retailer needs several layers to account for organizational size and resulting complexity. We discuss how to organize for a changed approach in dealing with complexity in subsequent sections.

Technical discussion

Optimization-derived supply chain network designs match supply and demand to the best feasible extent at the lowest possible cost, while satisfying a set of operational constraints to ensure realistic implementation. It is most pertinent for situations that exhibit a large variability of potential decisions and their inter-dependencies. How one decision affects others and what subset of decisions is best overall, is impossible for a human brain to assess and decide on using mental simulation. For example, it is common to solve network optimizations for millions of potential decision permutations. We are seeing that the objectives of supply chain optimizations are extending beyond costs (e.g., maximization of delivery speed and time to market, minimization of carbon emissions, and traffic avoidance). This results in multi-objective network optimization: finding acceptable trade-offs between competing metrics such as cost and speed, which further exacerbates combinational decision complexity. Mathematical optimization has been the traditional go-to approach to find the best supply chain network configurations. However, we also observe the complementary usage of other analytical approaches, such as dynamic simulations and machine learning (ML) that can be used to expand the solution space of network optimizations, enrich its inputs, and assess stochastic variability to provide better quality or more granular decisions.

Optimization techniques and technology

Both the mathematical optimization and algorithmic optimization fields have advanced significantly in the last decades. The scale and complexity of the problems that can be solved to optimality or near optimality grew exponentially thanks to research advancement coupled with computing power. This advancement facilitates integration of complicated business rules into models and algorithms. While such complications used to be managed only at the implementation stage traditionally, these rules used to hinder the benefits of optimization derived supply chain network designs.

The balanced layering approach also facilitates the optimized use of optimization techniques among the layers. The modern techniques make it possible to attack specific challenges with a specific recipe. For example,

• computing power and parallel processing have contributed to solving large scale end-to-end overarching supply chain network models
• through collateral developments in data analytics, stochastic optimization promotes high-levels of uncertainty to accelerate solutions of stochastic last mile routing

Therefore, the balanced layer can align to the optimization technology required to solve the corresponding layer problem.

There are also recent technological advances that are likely to further speed up optimizations of the future and support more complex models. For example Combinatorial Optimization with Physics-Inspired Graph Neural Networks can solve large-scale combinatorial optimization problems with quantum-native models helping our customers get quantum-ready and traditional supply chain problems such as the Travelling Salesperson Problem can be solved at very-large scale with Deep Reinforcement Learning with a potential to bring together artificial intelligence and human assessment. However, in the meanwhile, we believe that our complexity layering approach can make a difference for current supply chain network decision making. For example, we are using this approach for optimizing Amazon networks and it proves useful for its complexity and scale.

Organize for a change in approach

Traditional organizational approaches around deploying operations research (OR)-based tools and skillsets reveal clear limitations when dealing with network optimization complexities. Companies dealing with multi-objective problems came to an understanding that technology is only one part of a total solution and broader organization set-up, alignment, and workforce skillsets are critical in responding to rapidly changing supply chain network objectives. Organizations that look to succeed in dealing with network complexities and multi-objective problems need to take a holistic approach to re-assess numerous aspects of their supply chain people model by deep review of 1) organizational model and set-up, 2) workforce skillsets, and 3) organizational objectives alignment across key supply chain functions. Successful approaches include structuring specific functions around smaller sets of processes (e.g., micro-services as components of our proposed layers) that simplify staff objectives. Consequently, skillset development and enrichment to further educate supply chain professionals on how math optimization algorithms operate, what matters for solution speed and quality, scenario design, and newly emerging experimental workstreams such as ML and re-enforcement learning as part of advanced analytics, etc. prove valuable in solving large and complex network problems. Lastly, decision tree development for solving large network problems that cross multiple functional areas and underpinned by our layering approach help bolster organizational alignment and improve speed of the decision process. While many traditional approaches focused on just tools, the organizational component is an integral part in dealing with network optimization complexity and, thus, cannot be overlooked in a broader solution scheme to ensure success.

Conclusion

In this post, we discussed why traditional approaches to optimization tend to take long time and not necessarily accommodate end-to-end supply chain decision making. Businesses often try to compress too much complexity into a single network model, which makes it too challenging in terms of computational complexity and prohibits expanding it to cover additional supply chain functions. We showed how our layering approach helps to balance computational complexity that keeps it manageable and supports end-to-end analysis by setting up layers with different scope, planning horizons, and levels of uncertainty. We also touched on the need to re-assess organizational structures, alignment, and skills to ensure successful transformations. We believe that our joint technological and organizational approach is particularly suitable and beneficial for larger companies that wrestle with various types of complexity and uncertainty because of their size (e.g., Amazon). As we are eager to learn about your approaches to complexity in supply chain network optimizations, please leave your opinions in the comments. If you also wish to explore how AWS could support you in cutting through the complexity in your supply chain, then please reach out to your account manager to set up a discovery workshop with the AWS Supply Chain, Transportation, and Logistics business unit.