Explore quantum computational advantage with Xanadu’s Borealis device on Amazon Braket

Today, we are excited to launch Borealis, a new quantum processing unit (QPU) on Amazon Braket. Borealis – a special-purpose QPU built by Xanadu – is the first publicly available quantum computer with a claim to quantum computational advantage (sometimes referred to as quantum supremacy or quantum advantage) in a peer-reviewed study.

With this launch, we expand the range of quantum technologies customers can access on Amazon Braket to now include a photonic quantum device, in addition to the existing superconducting and ion-trap devices. Borealis brings state-of-the-art photonic quantum computing hardware to researchers around the world, enabling them to analyze the quantum advantage claim, devise their own experiments, and explore potential applications of Gaussian Boson Sampling (GBS), a special-purpose modality of continuous variable (CV) quantum computing. CV devices store and process quantum information in continuous degrees of freedom, the so-called qumodes, in contrast to the binary qubit representation used by most quantum computers.

Quantum advantage – a formidable challenge

Quantum advantage refers to the demonstration that a programmable quantum device can solve a problem that no classical computer – even the world’s fastest supercomputer – can solve in any feasible amount of time [1, 2]. The types of problems proposed for quantum advantage are not necessarily useful in the sense of solving industrially relevant computational problems. Instead, in this early stage of the technology, the focus is on artificial, carefully constructed mathematical challenges tailored to the capabilities of current quantum computers. Still, quantum advantage is a crucial technical milestone on the way to useful quantum computing. Most importantly, we know that a device that cannot demonstrate quantum advantage, for sure, cannot perform useful computations with quantum advantage – we can always just simulate the device on classical computers. As such, quantum advantage is a necessary, albeit not sufficient condition for quantum computing to solve industry relevant computational challenges faster than classical computers. On the other hand, since we generally cannot simulate quantum advantage devices anymore, they provide an opportunity to investigate heuristic algorithms, i.e., applications based on trial and error which are hard to study theoretically, at a scale inaccessible to classical computers.

Demonstrating quantum advantage itself is a formidable challenge and subject to intense scrutiny by the research community. First, how do you verify that the answer your quantum computer outputs is the correct one? By definition, you can’t use a classical computer to check and validate the answer. Second, proving a negative is always difficult. How do you demonstrate that there really is no classical approach out there that would be able to solve the problem as well? In practice, this means that quantum advantage is not a hard line in the sand. A quantum advantage claim often inspires new classical techniques that are more efficient in solving the problem, which in turn pushes the community to develop larger and more advanced quantum computing devices. By providing on-demand access to Borealis on Amazon Braket together with scalable, state-of-the-art classical compute on AWS, we want to encourage this healthy competition and accelerate innovation for both classical and quantum computational approaches.

But first, let’s take a closer look at the experiment conducted by the team of researchers at Xanadu and NIST that resulted in the Borealis advantage claim.

Quantum advantage with Borealis, a programmable, photonic QPU

In the study, published in Nature, the researchers carry out Gaussian Boson Sampling (GBS) with Borealis. GBS was one of the first proposals [3] on how to demonstrate quantum advantage using special-purpose, programmable quantum devices. The problem is to sample from a photon number output distribution after sending coherent states of light through an optical interferometer. There are strong, complexity theoretical arguments for why this task is hard for classical computers, i.e., the compute requirements grow exponentially with the number of optical modes in the interferometer. Also empirically, there are no known classical algorithms to efficiently sample from such output distributions.

Borealis is designed to do exactly that. A single laser source creates a train of 216 phase-locked, identical pulses of light with a 6 MHz clock rate. Each pulse, also referred to as a qumode, is squeezed, i.e., prepared in a quantum mechanical state that exhibits distinct characteristics in the photon number distribution. The qumodes, only distinguishable by their respective time signature, are then injected into a sequence of dynamically programmable, loop-based interferometers. These interferometers are at the heart of the GBS experiment, enabling entangling gates between the qumodes: Programmable beam splitters and phase shifters can be set to selectively route qumodes into optical delay lines so they interfere with subsequent pulses, a strategy called temporal multiplexing. As shown in Figure 1, using three different length delay loops (1τ, 6τ, and 36τ, where τ=167 ns), qumodes across the pulse train can be entangled. The first loop (1τ), hereby interferes two neighboring pulses, the second loop (6τ) interferes two pulses that are separated by 6 time steps, and the third loop (36τ) interferes two pulses that are separated by 36 time steps. This non-local interaction allows for the creation of complex quantum mechanical states which can be illustrated in a 3D array as seen at the top of Figure 1 (each dimension representing 1τ, 6τ, and 36τ gates respectively).

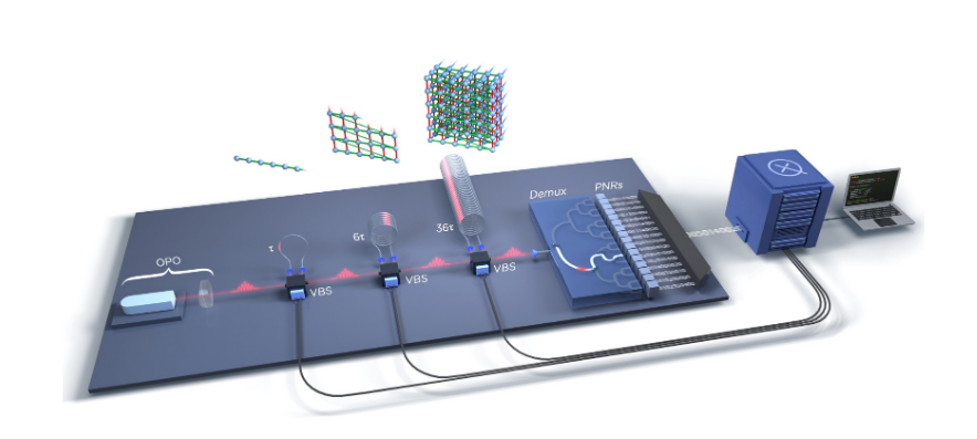
Figure 1: Physical architecture of the Borealis device. Squeezed laser pulses are generated inside an optical parametric oscillator (OPO) and injected into a sequence of three programmable loop interferometers. Each interferometer contains a variable beam splitter (VBS) that can delay pulses by 1τ, 6τ, and 36τ, respectively, to interfere them with subsequent pulses for entanglement creation. Finally, the state of the system is read out in the photon number basis using an array of photon-number resolving detectors (PNRs)

Interestingly, despite the state being highly entangled, it is still relatively easy to simulate, since the input states are Gaussian and there are efficient descriptions of such states under linear transformations (such as performed by beam splitters and phase shifters) even for a large number of modes. However, the last part of the experiment, the sampling, breaks this description. In this final step, the state of the system is measured using an array of photon-number resolving detectors based on superconducting transition edge sensors. This non-linear operation projects the state onto a photon number state, or Fock state, which cannot be described anymore as a Gaussian state, and the classical description breaks down. Due to the entanglement in the system, the probabilities of the outcomes from each of the 216 squeezed-state qumodes are not independent, and computing them quickly becomes intractable on a classical computer.

So, how do we know that the device really performed GBS? We cannot calculate and verify the full sampling results on a classical computer – after all, the fact that this computation is hard is the whole point of the quantum advantage experiment. Instead, the authors consider certain computable signatures of the experimental results, and then show that these signatures align best with the theoretical predictions for GBS in comparison with alternative, plausible hypotheses. For instance, the experimentally measured photon number distribution (Figure 2 insert, green line) matches the predictions for GBS (blue line) much better than the predictions for alternative hypotheses. The authors compared other signatures, such as the second order cumulants, with the same findings.

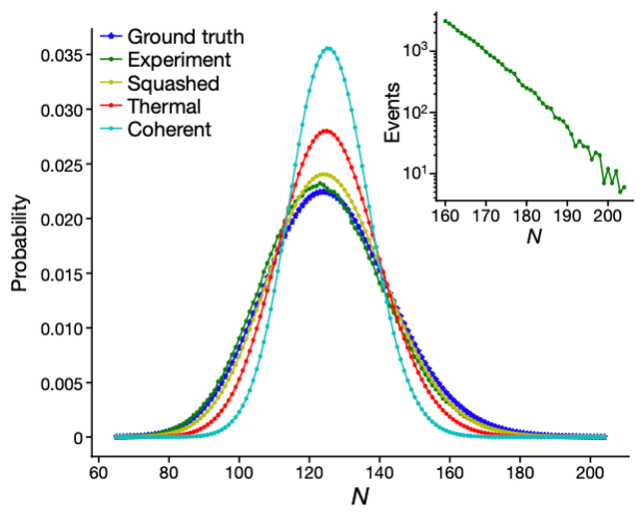
Figure 2: The probability distribution of total photon counts of 1 million shots from the experiment (green), plotted against the predictions for GBS (blue) and other alternative hypotheses. The inset shows that there are a significant number of shots with a large (>160) number of photon counts.

The paper also estimates the required classical simulation time on the Fugaku supercomputer, using state-of-the-art algorithms, for single samples from the Borealis device in Figure 3 (pictured together with the earlier Jiuzhang 2.0 photonic quantum computer [4]). By the authors’ assessment it would take, on average, 9000 years of classical computation time on Fugaku to generate a single sample produced from the experiment, compared to only 36 microseconds on Borealis. Of course, it remains to be seen if researchers can devise other, more efficient algorithms, but the computational gap between the classical and quantum computations claimed in the publication (9000 years vs. 36 microseconds) would put Borealis well into the quantum advantage regime.

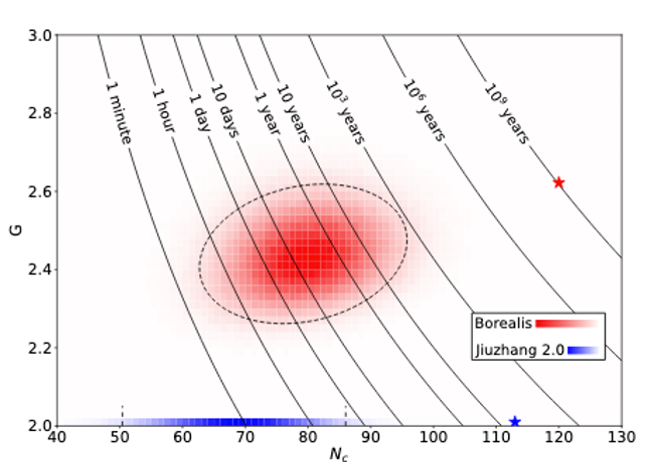
Figure 3: Estimated classical simulation times on Fugaku for the samples generated in the quantum advantage experiment on Borealis (red) and Jiuzhang 2.0 (blue). G and Nc are parameters characterizing the complexity of each sample that increase as the photon count increases. The stars represent the highest complexity samples generated by each of the devices.

Borealis on Braket

With today’s launch, Amazon Braket provides customers with on-demand access to Borealis, the very device that was used in the quantum advantage demonstration. Researchers can analyze and study quantum advantage experiments and, with Amazon Braket tightly integrated into AWS, they have scalable, state-of-the art compute solutions at their fingertips to also innovate on classical approaches to the GBS sampling problem.

Borealis is the first publicly accessible device with a peer-reviewed quantum advantage claim, giving customers access, for the first time, to quantum computations that cannot be simulated on a classical device. Several proposals [5] have shown that certain graph-type problems can be mapped onto a GBS formulation. While these applications of GBS are speculative and a potential quantum advantage for them uncertain, Borealis allows researchers to study these algorithms – for graphs that can be mapped to the Borealis qumode connectivity – at previously inaccessible scale. We hope that providing a wide range of scientists with access to state-of-the-art GBS will inspire new research and we are excited to see how the community will advance the knowledge of this field.

Customers can access Borealis on Braket by using Strawberry Fields, Xanadu’s open source library for photonic quantum computing. Like in the experiment above, you can specify different operations to be applied to each qumode with some restrictions arising from the physical architecture of the device. You can define the initial squeezing parameter of each qumode by applications of Sgates on each qumode at the beginning of the program. Then, for each of the three loop interferometers and for each qumode, you can specify a single qumode rotation angle via Rgates, as well as the transmittivity of BSgates between the qumode and the time-delayed qumode given by the delay of the respective interferometer.

Let’s take a look how this is done in practice. You start off by specifying the target device:

import strawberryfields as sf
import numpy as np
from braket.strawberryfields_plugin import BraketEngine

eng = BraketEngine("arn:aws:braket:us-east-1::device/qpu/xanadu/Borealis")
device = eng.device

Next, you need to specify arguments for each of the quantum gates at each time slice. For the quantum advantage experiment, random arguments can easily be generated using a few helper functions but you can customize the parameters according to your experiment.

from strawberryfields.tdm import borealis_gbs, get_mode_indices

gate_args_list = borealis_gbs(device, modes=216, squeezing="high")
delays = [1, 6, 36]
n, N = get_mode_indices(delays)

A quantum circuit on Borealis looks like the following:

from strawberryfields.ops import Sgate, Rgate, BSgate, MeasureFock

prog = sf.TDMProgram(N)
with prog.context(*gate_args_list) as (p, q):
   Sgate(p[0]) | q[n[0]]
   for i in range(len(delays)):
       Rgate(p[2 * i + 1]) | q[n[i]]
       BSgate(p[2 * i + 2], np.pi / 2) | (q[n[i + 1]], q[n[i]])
    MeasureFock() | q[0]

All Borealis circuits must be in the format above; while you have the flexibility to adjust the gate parameters freely, the sequence of gates has to follow the structure above since the gates are closely tied to the physical interferometer layout of the device. Finally, you can run the circuit like this:

shots = 250000
results = eng.run(prog, shots=shots, crop=True)
samples = results.samples

By running this code, you will have completed your own quantum advantage experiment using Amazon Braket!

Conclusion

With today’s launch, Amazon Braket provides customers with on-demand access to Borealis, a programmable, photonic QPU that has claimed quantum advantage through GBS in a peer-reviewed study. You can use Borealis on Amazon Braket using the Braket SDK and Strawberry Fields. You can explore the device capabilities and view the availability times of Borealis in the Braket console. The device is accessible in the US East (N. Virginia) Region. Refer to this quickstart guide to get started with running circuits on Borealis. For more details see this tutorial, as well as Xanadu’s blog post.

We invite academic researchers interested in testing the quantum advantage claim or exploring applications of GBS to apply for research credits through the AWS Cloud Credits for Research program.