AWS Machine Learning Blog
Learn how Amazon SageMaker Clarify helps detect bias
Bias detection in data and model outcomes is a fundamental requirement for building responsible artificial intelligence (AI) and machine learning (ML) models. Unfortunately, detecting bias isn’t an easy task for the vast majority of practitioners due to the large number of ways in which it can be measured and different factors that can contribute to a biased outcome. For instance, an imbalanced sampling of the training data may result in a model that is less accurate for certain subsets of the data. Bias may also be introduced by the ML algorithm itself—even with a well-balanced training dataset, the outcomes might favor certain subsets of the data as compared to the others.
To detect bias, you must have a thorough understanding of different types of bias and the corresponding bias metrics. For example, at the time of this writing, Amazon SageMaker Clarify offers 21 different metrics to choose from.
In this post, we use an income prediction use case (predicting user incomes from input features like education and number of hours worked per week) to demonstrate different types of biases and the corresponding metrics in SageMaker Clarify. We also develop a framework to help you decide which metrics matter for your application.
Introduction to SageMaker Clarify
ML models are being increasingly used to help make decisions across a variety of domains, such as financial services, healthcare, education, and human resources. In many situations, it’s important to understand why the ML model made a specific prediction and also whether the predictions were impacted by bias.
SageMaker Clarify provides tools for both of these needs, but in this post we only focus on the bias detection functionality. To learn more about explainability, check out Explaining Bundesliga Match Facts xGoals using Amazon SageMaker Clarify.
SageMaker Clarify is a part of Amazon SageMaker, which is a fully managed service to build, train, and deploy ML models.
Examples of questions about bias
To ground the discussion, the following are some sample questions that ML builders and their stakeholders may have regarding bias. The list consists of some general questions that may be relevant for several ML applications, as well as questions about specific applications like document retrieval.
You might ask, given the groups of interest in the training data (for example, men vs. women) which metrics should I use to answer the following questions:
- Does the group representation in the training data reflect the real world?
- Do the target labels in the training data favor one group over the other by assigning it more positive labels?
- Does the model have different accuracy for different groups?
- In a model whose purpose is to identify qualified candidates for hiring, does the model have the same precision for different groups?
- In a model whose purpose is to retrieve documents relevant to an input query, does the model retrieve relevant documents from different groups in the same proportion?
In the rest of this post, we develop a framework for how to consider answering these questions and others through the metrics available in SageMaker Clarify.
Use case and context
This post uses an existing example of a SageMaker Clarify job from the Fairness and Explainability with SageMaker Clarify notebook and explains the generated bias metric values. The notebook trains an XGBoost model on the UCI Adult dataset (Dua, D. and Graff, C. (2019). UCI Machine Learning Repository. Irvine, CA: University of California, School of Information and Computer Science).
The ML task in this dataset is to predict whether a person has a yearly income of more or less than $50,000. The following table shows some instances along with their features. Measuring bias in income prediction is important because we could use these predictions to inform decisions like discount offers and targeted marketing.
Bias terminology
Before diving deeper, let’s review some essential terminology. For a complete list of terms, see Amazon SageMaker Clarify Terms for Bias and Fairness.
- Label – The target feature that the ML model is trained to predict. An observed label refers to the label value observed in the data used to train or test the model. A predicted label is the value predicted by the ML model. Labels could be binary, and are often encoded as 0 and 1. We assume 1 to represent a favorable or positive label (for example, income more than or equal to $50,000), and 0 to represent an unfavorable or negative label. Labels could also consist of more than two values. Even in these cases, one or more of the values constitute favorable labels. For the sake of simplicity, this post only considers binary labels. For details on handling labels with more than two values and labels with continuous values (for example, in regression), see Amazon AI Fairness and Explainability Whitepaper.
- Facet – A column or feature with respect to which bias is measured. In our example, the facet is
sexand takes two values:womanandman, encoded asfemaleandmalein the data (this data is extracted from the 1994 Census and enforces a binary option). Although the post considers a single facet with only two values, for more complex cases involving multiple facets or facets with more than two values, see Amazon AI Fairness and Explainability Whitepaper. - Bias – A significant imbalance in the input data or model predictions across different facet values. What constitutes “significant” depends on your application. For most metrics, a value of 0 implies no imbalance. Bias metrics in SageMaker Clarify are divided into two categories:
- Pretraining – When present, pretraining bias indicates imbalances in the data only.
- Posttraining – Posttraining bias additionally considers the predictions of the models.
Let’s examine each category separately.
Pretraining bias
Pretraining bias metrics in SageMaker Clarify answer the following question: Do all facet values have equal (or similar) representation in the data? It’s important to inspect the data for pretraining bias because it may translate into posttraining bias in the model predictions. For instance, a model trained on imbalanced data where one facet value appears very rarely can exhibit substantially worse accuracy for that facet value. Equal representation can be calculated over the following:
- The whole training data irrespective of the labels
- The subset of the training data with positive labels only
- Each label separately
The following figure provides a summary of how each metric fits into each of the three categories.
Some categories consist of more than one metric. The basic metrics (grey boxes) answer the question about bias in that category in the simplest form. Metrics in white boxes additionally cover special cases (for example, Simpson’s paradox) and user preferences (for example, focusing on certain parts of the population when computing predictive performance).
Facet value representation irrespective of labels
The only metric in this category is Class Imbalance (CI). The goal of this metric is to measure if all the facet values have equal representation in the data.
CI is the difference in the fraction of the data constituted by the two facet values. In our example dataset, for the facet sex, the breakdown (shown in the pie chart) shows that women constitute 32.4% of the training data, whereas men constitute 67.6%. As a result:
CI = 0.676 - 0.324 = 0.352
A severely high class imbalance could lead to worse predictive performance for the facet value with smaller representation.
Facet value representation at the level of positive labels only
Another way to measure equal representation is to check whether all facet values contain a similar fraction of samples with positive observed labels. Positive labels consist of favorable outcomes (for example, loan granted, selected for the job), so analyzing positive labels separately helps assess if the favorable decisions are distributed evenly.
In our example dataset, the observed labels break down into positive and negative values, as shown in the following figure.
11.4% of all women and 31.4% of all men have the positive label (dark shaded region in the left and right bars). The Difference in Positive Proportions in Labels (DPL) measures this difference.
DPL = 0.314 - 0.114 = 0.20
The advanced metric in this category, Conditional Demographic Disparity in Labels (CDDL), measures the differences in the positive labels, but stratifies them with respect to another variable. This metric helps control for the Simpson’s paradox, a case where a computation over the whole data shows bias, but the bias disappears when grouping the data with respect to some side-information.
The 1973 UC Berkeley Admissions Study provides an example. According to the data, men were admitted at a higher rate than women. However, when examined at the level of individual university departments, women were admitted at similar or higher rate at each department. This observation can be explained by the Simpson’s paradox, which arose here because women applied to schools that were more competitive. As a result, fewer women were admitted overall compared to men, even though school by school they were admitted at a similar or higher rate.
For more detail on how CDDL is computed, see Amazon AI Fairness and Explainability Whitepaper.
Facet value representation at the level of each label separately
Equality in representation can also be measured for each individual label, not just the positive label.
Metrics in this category compute the difference in the label distribution of different facet values. The label distribution for a facet value contains all the observed label values, along with the fraction of samples with that label’s value. For instance, in the figure showing labels distributions, 88.6% of women have a negative observed label and 11.4% have a positive observed label. So the label distribution for women is [0.886, 0.114] and for men is [0.686, 0.314].
The basic metric in this category, Kullback-Leibler divergence (KL), measures this difference as:
KL = [0.686 x log(0.686/0.886)] + [0.314 x log(0.314/0.114)] = 0.143
The advanced metrics in this category, Jensen-Shannon divergence (JS), Lp-norm (LP), Total Variation Distance (TVD), and Kolmogorov-Smirnov (KS), also measure the difference between the distributions but have different mathematical properties. Barring special cases, they will deliver insights similar to KL. For example, although the KL value can be infinity when a facet value contains no samples with a certain labels (for example, no men with a negative label), JS avoids these infinite values. For more detail into these differences, see Amazon AI Fairness and Explainability Whitepaper.
Relationship between DPL (Category 2) and distribution-based metrics of KL/JS/LP/TVD/KS (Category 3)
Distribution-based metrics are more naturally applicable to non-binary labels. For binary labels, owing to the fact that imbalance in the positive label can be used to compute the imbalance in negative label, the distribution metrics deliver the same insights as DPL. Therefore, you can just use DPL in such cases.
Posttraining bias
Posttraining bias metrics in SageMaker Clarify help us answer two key questions:
- Are all facet values represented at a similar rate in positive (favorable) model predictions?
- Does the model have similar predictive performance for all facet values?
The following figure shows how the metrics map to each of these questions. The second question can be further broken down depending on which label the performance is measured with respect to.
Equal representation in positive model predictions
Metrics in this category check if all facet values contain a similar fraction of samples with positive predicted label by the model. This class of metrics is very similar to the pretraining metrics of DPL and CDDL—the only difference is that this category considers predicted labels instead of observed labels.
In our example dataset, 4.5% of all women are assigned the positive label by the model, and 13.7% of all men are assigned the positive label.
The basic metric in this category, Difference in Positive Proportions in Predicted Labels (DPPL), measures the difference in the positive class assignments.
DPPL = 0.137 - 0.045 = 0.092
Notice how in the training data, a higher fraction of men had a positive observed label. In a similar manner, a higher fraction of men are assigned a positive predicted label.
Moving on to the advanced metrics in this category, Disparate Impact (DI) measures the same disparity in positive class assignments, but instead of the difference, it computes the ratio:
DI = 0.045 / 0.137 = 0.328
Both DI and DPPL convey qualitatively similar insights but differ at some corner cases. For instance, ratios tend to explode to very large numbers if the denominator is small. Take an example of the numbers 0.1 and 0.0001. The ratio is 0.1/0.0001 = 10,000 whereas the difference is 0.1 – 0.0001 ≈ 0.1. Unlike the other metrics where a value of 0 implies no bias, for DI, no bias corresponds to a value of 1.
Conditional Demographic Disparity in Predicted Labels (CDDPL) measures the disparity in facet value representation in the positive label, but just like the pretraining metric of CDDL, it also controls for the Simpson’s paradox.
Counterfactual Fliptest (FT) measures if similar samples from the two facet values receive similar decisions from the model. A model assigning different decisions to two samples that are similar to each other but differ in the facet values could be considered biased against the facet value being assigned the unfavorable (negative) label. Given the first facet value (women), it assesses whether similar members with the other facet value (men) have a different model prediction. Similar members are chosen based on the k-nearest neighbor algorithm.
Equal performance
The model predictions might have similar representation in positive labels from different facet values, yet the model performance on these groups might significantly differ. In many applications, having a similar predictive performance across different facet values can be desirable. The metrics in this category measure the difference in predictive performance across facet values.
Because the data can be sliced in many different ways based on the observed or predicted labels, there are many different ways to measure predictive performance.
Equal predictive performance irrespective of labels
You could consider the model performance on the whole data, irrespective of the observed or the predicted labels – that is, the overall accuracy.
The following figures shows how the model classifies inputs from the two facet values in our example dataset. True negatives (TN) are cases where both the observed and predicted label were 0. False positives (FP) are misclassifications where the observed label was 0 but the predicted label was 1. True positives (TP) and false negatives (FN) are defined similarly.
 |
 |
For each facet value, the overall model performance, that is, the accuracy for that facet value, is:
Accuracy = (TN + TP) / (TN + FP + FN + TP)
With this formula, the accuracy for women is 0.930 and for men is 0.815. This leads to the only metric in this category, Accuracy Difference (AD):
AD = 0.815 - 0.930 = -0.115
AD = 0 means that the accuracy for both groups is the same. Larger (positive or negative) values indicate larger differences in accuracy.
Equal performance on positive labels only
You could restrict the model performance analysis to positive labels only. For instance, if the application is about detecting defects on an assembly line, it may be desirable to check that non-defective parts (positive label) of different kinds (facet values) are classified as non-defective at the same rate. This quantity is referred to as recall, or true positive rate:
Recall = TP / (TP + FN)
In our example dataset, the recall for women is 0.389, and the recall for men is 0.425. This leads to the basic metric in this category, the Recall Difference (RD):
RD = 0.425 - 0.389 = 0.036
Now let’s consider the three advanced metrics in this category, see which user preferences they encode, and how they differ from the basic metric of RD.
First, instead of measuring the performance on the positive observed labels, you could measure it on the positive predicted labels. Given a facet value, such as women, and all the samples with that facet value that are predicted to be positive by the model, how many are actually correctly classified as positive? This quantity is referred to as acceptance rate (AR), or precision:
AR = TP / (TP + FP)
In our example, the AR for women is 0.977, and the AR for men is 0.970. This leads to the Difference in Acceptance Rate (DAR):
DAR = 0.970 - 0.977 = -0.007
Another way to measure bias is by combining the previous two metrics and measuring how many more positive predictions the models assign to a facet value as compared to the observed positive labels. SageMaker Clarify measures this advantage by the model as the ratio between the number of observed positive labels for that facet value, and the number of predicted positive labels, and refers to it as conditional acceptance (CA):
CA = (TP + FN) / (TP + FP)
In our example, the CA for women is 2.510 and for men is 2.283. The difference in CA leads to the final metric in this category, Difference in Conditional Acceptance (DCA):
DCA = 2.283 - 2.510 = -0.227
Equal performance on negative labels only
In a manner similar to positive labels, bias can also be computed as the performance difference on the negative labels. Considering negative labels separately can be important in certain applications. For instance, in our defect detection example, we might want to detect defective parts (negative label) of different kinds (facet value) at the same rate.
The basic metric in this category, specificity, is analogous to the recall (true positive rate) metric. Specificity computes the accuracy of the model on samples with this facet value that have an observed negative label:
Specificity = TN / (TN + FP)
In our example (see the confusion tables), the specificity for women and men is 0.999 and 0.994, respectively. Consequently, the Specificity Difference (SD) is:
SD = 0.994 - 0.999 = -0.005
Moving on, just like the acceptance rate metric, the analogous quantity for negative labels—the rejection rate (RR)—is:
RR = TN / (TN + FN)
The RR for women is 0.927 and for men is 0.791, leading to the Difference in Rejection Rate (DRR) metric:
DRR = 0.927 - 0.791 = -0.136
Finally, the negative label analogue of conditional acceptance, the conditional rejection (CR), is the ratio between the number of observed negative labels for that facet value, and the number of predicted negative labels:
CR = (TN + FP) / (TN + FN)
The CR for women is 0.928 and for men is 0.796. The final metric in this category is Difference in Conditional Rejection (DCR):
DCR = 0.796 - 0.928 = 0.132
Equal performance on positive vs. negative labels
SageMaker Clarify combines the previous two categories by considering the model performance ratio on the positive and negative labels. Specifically, for each facet value, SageMaker Clarify computes the ration between false negatives (FN) and false positives (FP). In our example, the FN/FP ratio for women is 679/10 = 67.9 and for men is 3678/84 = 43.786. This leads to the Treatment Equality (TE) metric, which measures the difference between the FP/FN ratio:
TE = 67.9 - 43.786 = 24.114
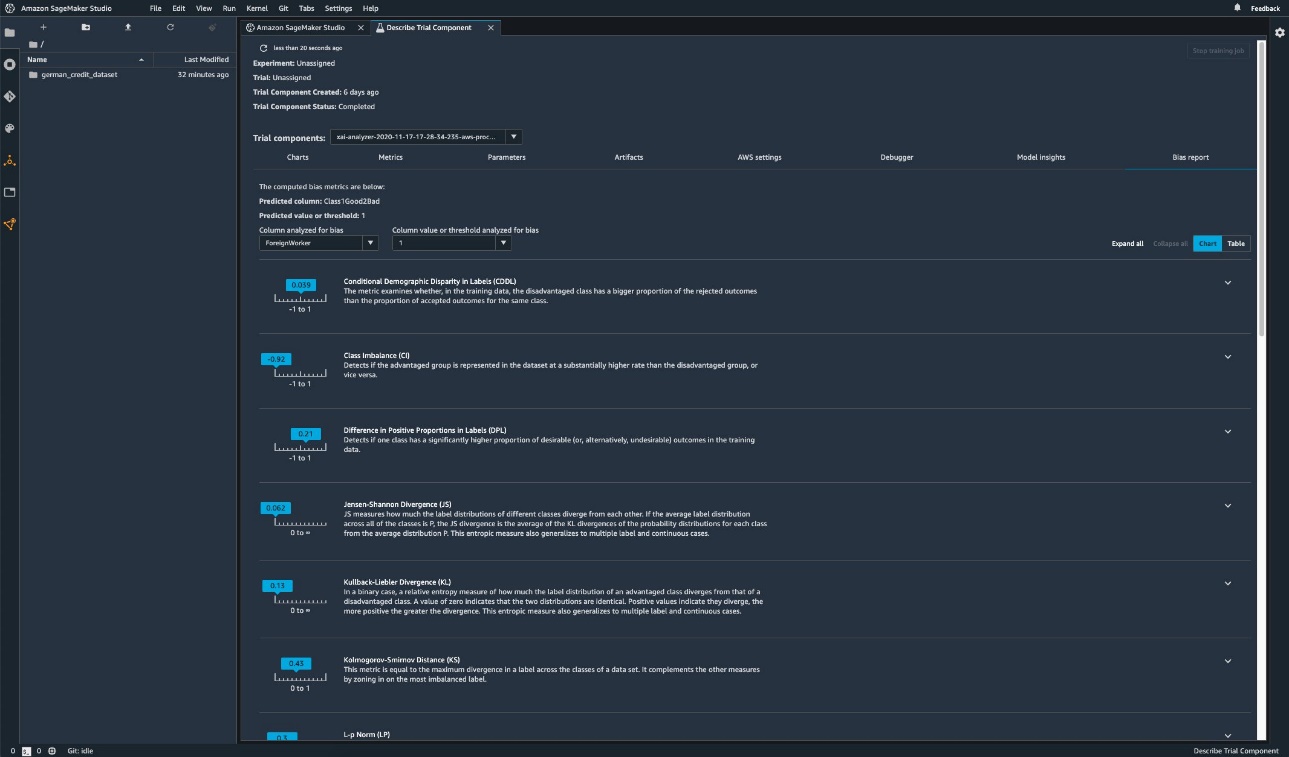
The following screenshot shows how you can use SageMaker Clarify with Amazon SageMaker Studio to show the values as well as ranges and short descriptions of different bias metrics.
Questions about bias: Which metrics to start with?
Recall the sample questions about bias at the start of this post. Having gone through the metrics from different categories, consider the questions again. To answer the first question, which concerns the representations of different groups in the training data, you could start with the Class Imbalance (CI) metric. Similarly, for the remaining questions, you can start by looking into Difference in Positive Proportions in Labels (DPL), Accuracy Difference (AD), Difference in Acceptance Rate (DAR), and Recall Difference (RD), respectively.
Bias without facet values
For the ease of exposition, this description of posttraining metrics excluded the Generalized Entropy Index (GE) metric. This metric measures bias without considering the facet value, and can be helpful in assessing how the model errors are distributed. For details, refer to Generalized entropy (GE).
Conclusion
In this post, you saw how the 21 different metrics in SageMaker Clarify measure bias at different stages of the ML pipeline. You learned about various metrics via an income prediction use case, how to choose metrics for your use case, and which ones you could start with.
Get started with your responsible AI journey by assessing bias in your ML models by using the demo notebook Fairness and Explainability with SageMaker Clarify. You can find the detailed documentation for SageMaker Clarify, including the formal definition of metrics, at What Is Fairness and Model Explainability for Machine Learning Predictions. For the implementation of the bias metrics, refer to the aws-sagemaker-clarify GitHub repository. For a detailed discussion including limitations, refer to Amazon AI Fairness and Explainability Whitepaper.
About the authors
 Bilal Zafar is an Applied Scientist at AWS, working on Fairness, Explainability and Security in Machine Learning.
Bilal Zafar is an Applied Scientist at AWS, working on Fairness, Explainability and Security in Machine Learning.
 Denis V. Batalov is a 17-year Amazon veteran and a PhD in Machine Learning, Denis worked on such exciting projects as Search Inside the Book, Amazon Mobile apps and Kindle Direct Publishing. Since 2013 he has helped AWS customers adopt AI/ML technology as a Solutions Architect. Currently, Denis is a Worldwide Tech Leader for AI/ML responsible for the functioning of AWS ML Specialist Solutions Architects globally. Denis is a frequent public speaker, you can follow him on Twitter @dbatalov.
Denis V. Batalov is a 17-year Amazon veteran and a PhD in Machine Learning, Denis worked on such exciting projects as Search Inside the Book, Amazon Mobile apps and Kindle Direct Publishing. Since 2013 he has helped AWS customers adopt AI/ML technology as a Solutions Architect. Currently, Denis is a Worldwide Tech Leader for AI/ML responsible for the functioning of AWS ML Specialist Solutions Architects globally. Denis is a frequent public speaker, you can follow him on Twitter @dbatalov.
 Michele Donini is a Sr Applied Scientist at AWS. He leads a team of scientists working on Responsible AI and his research interests are Algorithmic Fairness and Explainable Machine Learning.
Michele Donini is a Sr Applied Scientist at AWS. He leads a team of scientists working on Responsible AI and his research interests are Algorithmic Fairness and Explainable Machine Learning.