AWS Machine Learning Blog
Optimize F1 aerodynamic geometries via Design of Experiments and machine learning
FORMULA 1 (F1) cars are the fastest regulated road-course racing vehicles in the world. Although these open-wheel automobiles are only 20–30 kilometers (or 12–18 miles) per-hour faster than top-of-the-line sports cars, they can speed around corners up to five times as fast due to the powerful aerodynamic downforce they create. Downforce is the vertical force generated by the aerodynamic surfaces that presses the car towards the road, increasing the grip from the tires. F1 aerodynamicists must also monitor the air resistance or drag, which limits straight-line speed.
The F1 engineering team is in charge of designing the next generation of F1 cars and putting together the technical regulation for the sport. Over the last 3 years, they have been tasked with designing a car that maintains the current high levels of downforce and peak speeds, but is also not adversely affected by driving behind another car. This is important because the previous generation of cars can lose up to 50% of their downforce when racing closely behind another car due to the turbulent wake generated by wings and bodywork.
Instead of relying on time-consuming and costly track or wind tunnel tests, F1 uses Computational Fluid Dynamics (CFD), which provides a virtual environment to study the flow of fluids (in this case the air around the F1 car) without ever having to manufacture a single part. With CFD, F1 aerodynamicists test different geometry concepts, assess their aerodynamic impact, and iteratively optimize their designs. Over the past 3 years, the F1 engineering team has collaborated with AWS to set up a scalable and cost-efficient CFD workflow that has tripled the throughput of CFD runs and cut the turnaround time per run by half.
F1 is in the process of looking into AWS machine learning (ML) services such as Amazon SageMaker to help optimize the design and performance of the car by using the CFD simulation data to build models with additional insights. The aim is to uncover promising design directions and reduce the number of CFD simulations, thereby reducing the time taken to converge to optimal designs.
In this post, we explain how F1 collaborated with the AWS Professional Services team to develop a bespoke Design of Experiments (DoE) workflow powered by ML to advise F1 aerodynamicists on which design concepts to test in CFD to maximize learning and performance.
Problem statement
When exploring new aerodynamic concepts, F1 aerodynamicists sometimes employ a process called Design of Experiments (DoE). This process systematically studies the relationship between multiple factors. In the case of a rear wing, this might be wing chord, span, or camber, with respect to aerodynamic metrics such as downforce or drag. The goal of a DoE process is to efficiently sample the design space and minimize the number of candidates tested before converging to an optimal result. This is achieved by iteratively changing multiple design factors, measuring the aerodynamic response, studying the impact and relationship between factors, and then continuing testing in the most optimum or informative direction. In the following figure, we present an example rear wing geometry that F1 has kindly shared with us from their UNIFORM baseline. Four design parameters which F1 aerodynamicists could investigate in a DoE routine are labeled.
In this project, F1 worked with AWS Professional Services to investigate using ML to enhance DoE routines. Traditional DoE methods require a well-populated design space in order to understand the relationship between design parameters and therefore rely on a large number of upfront CFD simulations. ML regression models could use the results from previous CFD simulations to predict the aerodynamic response given the set of design parameters, as well as give you an indication of the relative importance of each design variable. You could use these insights to predict optimal designs and help designers converge to optimum solutions with fewer upfront CFD simulations. Secondly, you could use data science techniques to understand which regions in the design space haven’t been explored and could potentially hide optimal designs.
To illustrate the bespoke ML-powered DoE workflow, we walk through a real example of designing a front wing.
Designing a front wing
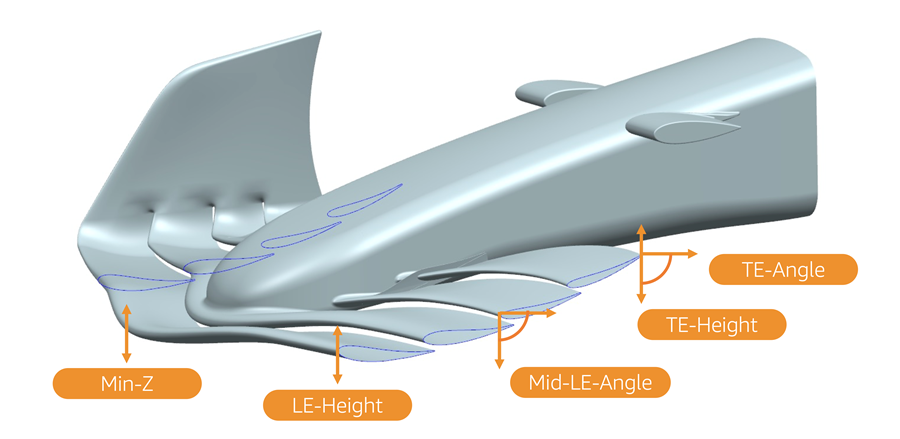
F1 cars rely on wings such as the front and rear wings to generate most of their downforce, which we refer to throughout this example by the coefficient Cz. Throughout this example, the downforce values have been normalized. In this example, F1 aerodynamicists used their domain expertise to parameterize the wing geometry as follows (refer to the following figure for a visual representation):
- LE-Height – Leading edge height
- Min-Z – Minimum ground clearance
- Mid-LE-Angle – Leading edge angle of the third element
- TE-Angle – Trailing edge angle
- TE-Height – Trailing edge height
This front wing geometry was shared by F1 and is part of the UNIFORM baseline.
These parameters were selected because they are sufficient to describe the main aspects of the geometry efficiently and because in the past, aerodynamic performance has shown notable sensitivity with respect to these parameters. The goal of this DoE routine was to find the combination of the five design parameters that would maximize aerodynamic downforce (Cz). The design freedom is also limited by setting maximum and minimum values to the design parameters, as shown in the following table.
| . | Minimum | Maximum |
| TE-Height | 250.0 | 300.0 |
| TE-Angle | 145.0 | 165.0 |
| Mid-LE-Angle | 160.0 | 170.0 |
| Min-Z | 5.0 | 50.0 |
| LE-Height | 100.0 | 150.0 |
Having established the design parameters, the target output metric, and the bounds of our design space, we have all we need to get started with the DoE routine. A workflow diagram of our solution is presented in the following image. In the following section, we dive deep into the different stages.
Initial sampling of the design space
The first step of the DoE workflow is to run in CFD an initial set of candidates that efficiently sample the design space and allow us to build the first set of ML regression models to study the influence of each feature. First, we generate a pool of N samples ![]() using Latin Hypercube Sampling (LHS) or a regular grid method. Then, we select k candidates to test in CFD by means of a greedy inputs algorithm, which aims to maximize the exploration of the design space. Starting with a baseline candidate (the current design), we iteratively select candidates furthest away from all the previously tested candidates. Suppose that we already tested k designs; for the remaining design candidates, we find the minimum distance d with respect to the tested k designs:
using Latin Hypercube Sampling (LHS) or a regular grid method. Then, we select k candidates to test in CFD by means of a greedy inputs algorithm, which aims to maximize the exploration of the design space. Starting with a baseline candidate (the current design), we iteratively select candidates furthest away from all the previously tested candidates. Suppose that we already tested k designs; for the remaining design candidates, we find the minimum distance d with respect to the tested k designs:
![]()
The greedy inputs algorithm selects the candidate that maximizes the distance in the feature space to the previously tested candidates:
![]()
In this DoE, we selected three greedy inputs candidates and ran those in CFD to assess their aerodynamic downforce (Cz). The greedy inputs candidates explore the bounds of the design space and at this stage, none of them proved superior to the baseline candidate in terms of aerodynamic downforce (Cz). The results of this initial round of CFD testing together with the design parameters are displayed in the following table.
| . | TE-Height | TE-Angle | Mid-LE-Angle | Min-Z | LE-Height | Normalized Cz |
| Baseline | 292.25 | 154.86 | 166 | 5 | 130 | 0.975 |
| GI 0 | 250 | 165 | 160 | 50 | 100 | 0.795 |
| GI 1 | 300 | 145 | 170 | 50 | 100 | 0.909 |
| GI 2 | 250 | 145 | 170 | 5 | 100 | 0.847 |
Initial ML regression models
The goal of the regression model is to predict Cz for any combination of the five design parameters. With such a small dataset, we prioritized simple models, applied model regularization to avoid overfitting, and combined the predictions of different models where possible. The following ML models were constructed:
- Ordinary Least Squares (OLS)
- Support Vector Regression (SVM) with an RBF kernel
- Gaussian Process Regression (GP) with a Matérn kernel
- XGBoost
In addition, a two-level stacked model was built, where the predictions of the GP, SVM, and XGBoost models are assimilated by a Lasso algorithm to produce the final response. This model is referred to throughout this post as the stacked model. To rank the predictive capabilities of the five models we described, a repeated k-fold cross validation routine was implemented.
Generating the next design candidate to test in CFD
Selecting which candidate to test next requires careful consideration. The F1 aerodynamicist must balance the benefit of exploiting options predicted by the ML model to provide high downforce with the cost of failing to explore uncharted regions of the design space, which may provide even higher downforce. For that reason, in this DoE routine, we propose three candidates: one performance-driven and two exploration-driven. The purpose of the exploration-driven candidates is also to provide additional data points to the ML algorithm in regions of the design space where the uncertainty around the prediction is highest. This in turn leads to more accurate predictions in the next round of design iteration.
Genetic algorithm optimization to maximize downforce
To obtain the candidate with the highest expected aerodynamic downforce, we could run a prediction over all possible design candidates. However, this wouldn’t be efficient. For this optimization problem, we use a genetic algorithm (GA). The goal is to efficiently search through a huge solution space (obtained via the ML prediction of Cz) and return the most optimal candidate. GAs are advantageous when the solution space is complex and non-convex, so that classical optimization methods such as gradient descent are an ineffective means to find a global solution. GA is a subset of evolutionary algorithms and inspired by concepts from natural selection, genetic crossover, and mutation to solve the search problem. Over a series of iterations (known as generations), the best candidates of an initially randomly selected set of design candidates are combined (much like reproduction). Eventually, this mechanism allows you to find the most optimal candidates in an efficient manner. For more information about GAs, refer to Using genetic algorithms on AWS for optimization problems.
Generating exploration-driven candidates
In generating what we term exploration-driven candidates, a good sampling strategy must be able to adapt to a situation of effect sparsity, where only a subset of the parameters significantly affects the solution. Therefore, the sampling strategy should spread out the candidates across the input design space but also avoid unnecessary CFD runs, changing variables that have little effect on performance. The sampling strategy must take into account the response surface predicted by the ML regressor. Two sampling strategies were employed to obtain exploration-driven candidates.
In the case of Gaussian Process Regressors (GP), the standard deviation ![]() of the predicted response surface can be used as an indication of the uncertainty of the model. The sampling strategy consists of selecting out of the pool of N samples
of the predicted response surface can be used as an indication of the uncertainty of the model. The sampling strategy consists of selecting out of the pool of N samples ![]() , the candidate that maximizes
, the candidate that maximizes ![]() . By doing so, we’re sampling in the region of the design space where the regressor is least confident about its prediction. In mathematical terms, we select the candidate that satisfies the following equation:
. By doing so, we’re sampling in the region of the design space where the regressor is least confident about its prediction. In mathematical terms, we select the candidate that satisfies the following equation:
Alternatively, we employ a greedy inputs and outputs sampling strategy, which maximizes both the distances in the feature space and in the response space between the proposed candidate and the already tested designs. This tackles the effect sparsity situation because candidates that modify a design parameter of little relevance have a similar response, and therefore the distances in the response surface are minimal. In mathematical terms, we select the candidate that satisfies the following equation, where the function f is the ML regression model:
Candidate selection, CFD testing, and optimization loop
At this stage, the user is presented with both performance-driven and exploration-driven candidates. The next step consists of selecting a subset of the proposed candidates, running CFD simulations with those design parameters, and recording the aerodynamic downforce response.
After this, the DoE workflow retrains the ML regression models, runs the genetic algorithm optimization, and proposes a new set of performance-driven and exploration-driven candidates. The user runs a subset of the proposed candidates and continues iterating in this fashion until the stopping criteria is met. The stopping criteria is generally met when a candidate deemed optimum is obtained.
Results
In the following figure, we record the normalized aerodynamic downforce (Cz) from the CFD simulation (blue) and the one predicted beforehand using the ML regression model of choice (pink) for each iteration of the DoE workflow. The goal was to maximize aerodynamic downforce (Cz). The first four runs (to the left of the red line) were the baseline and the three greedy inputs candidates outlined previously. From there on, a combination of performance-driven and exploration-driven candidates were tested. In particular, the candidates at iterations 6 and 8 were exploratory candidates, both showing lower levels of downforce than the baseline candidate (iteration 1). As expected, as we recorded more candidates, the ML prediction became increasingly accurate, as denoted by the decreasing distance between the predicted and actual Cz. At iteration 9, the DoE workflow managed to find a candidate with a similar performance to the baseline, and at iteration 12, the DoE workflow was concluded when the performance-driven candidate surpassed the baseline.
The final design parameters together with the resultant normalized downforce value is presented in the following table. The normalized downforce level for the baseline candidate was 0.975, whereas the optimum candidate for the DoE workflow recorded a normalized downforce level of 1.000. This is an important 2.5% relative increase.
For context, a traditional DoE approach with five variables would require 25 upfront CFD simulations before achieving a good enough fit to predict an optimum. On the other hand, this active learning approach converged to an optimum in 12 iterations.
| . | TE-Height | TE-Angle | Mid-LE-Angle | Min-Z | LE-Height | Normalized Cz |
| Baseline | 292.25 | 154.86 | 166 | 5 | 130 | 0.975 |
| Optimal | 299.97 | 156.79 | 166.27 | 5.01 | 135.26 | 1.000 |
Feature importance
Understanding the relative feature importance for a predictive model can provide a useful insight into the data. It can help feature selection with less important variables being removed, thereby reducing the dimensionality of the problem and potentially improving the predictive powers of the regression model, particularly in the small data regime. In this design problem, it provides F1 aerodynamicists an insight into which variables are the most sensitive and therefore require more careful tuning.
In this routine, we implemented a model-agnostic technique called permutation importance. The relative importance of each variable is measured by calculating the increase in the model’s prediction error after randomly shuffling the values for that variable alone. If a feature is important for the model, the prediction error increases greatly, and vice versa for lesser important features. In the following figure, we present the permutation importance for a Gaussian Process Regressor (GP) predicting aerodynamic downforce (Cz). The trailing edge height (TE-Height) was deemed the most important.
Conclusion
In this post, we explained how F1 aerodynamicists are using ML regression models in DoE workflows when designing novel aerodynamic geometries. The ML-powered DoE workflow developed by AWS Professional Services provides insights into which design parameters will maximize performance or explore uncharted regions in the design space. As opposed to iteratively testing candidates in CFD in a grid search fashion, the ML-powered DoE workflow is able to converge to optimal design parameters in fewer iterations. This saves both time and resources because fewer CFD simulations are required.
Whether you’re a pharmaceutical company looking to speed up chemical composition optimization or a manufacturing company looking to find the design dimensions for the most robust designs, DoE workflows can help reach optimal candidates more efficiently. AWS Professional Services is ready to supplement your team with specialized ML skills and experience to develop the tools to streamline DoE workflows and help you achieve better business outcomes. For more information, see AWS Professional Services, or reach out through your account manager to get in touch.
About the Authors
 Pablo Hermoso Moreno is a Data Scientist in the AWS Professional Services Team. He works with clients across industries using Machine Learning to tell stories with data and reach more informed engineering decisions faster. Pablo’s background is in Aerospace Engineering and having worked in the motorsport industry he has an interest in bridging physics and domain expertise with ML. In his spare time, he enjoys rowing and playing guitar.
Pablo Hermoso Moreno is a Data Scientist in the AWS Professional Services Team. He works with clients across industries using Machine Learning to tell stories with data and reach more informed engineering decisions faster. Pablo’s background is in Aerospace Engineering and having worked in the motorsport industry he has an interest in bridging physics and domain expertise with ML. In his spare time, he enjoys rowing and playing guitar.